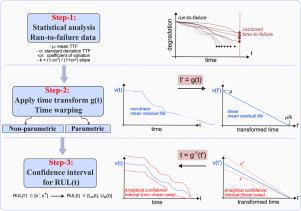
Analysis of RUL dynamics and uncertainty via time transformation

This work introduces a novel analytical method to analyze the dynamics of remaining useful life (RUL) and quantify uncertainty in its estimation. The approach employs a time transformation that makes the mean residual life (MRL) a linear function of transformed time, enabling the derivation of explicit RUL confidence bounds. Once mapped back to physical space, the bounds quantify aleatoric (stochastic) uncertainty in RUL and yield asymmetrical confidence intervals for both parametric and non-parametric lifetime distributions. The approach leverages a key feature of reliability distributions: the average RUL loss rate, $k$, in transformed time, facilitating a direct derivation of confidence bounds. In parametric cases, $k$ is uniquely defined by the reliability distribution parameters, while for non-parametric distributions, it is derived from data by estimating the coefficient of variation. Higher slopes indicate faster degradation, leading to narrower confidence intervals and lower RUL variance. The method’s applicability to stochastic processes and robustness under different data volumes are also investigated and discussed. The novel approach reveals heretofore unknown insights into classical reliability distributions. It is demonstrated through real-world applications, including LED reliability assessment, parallel system RUL estimation, and turbofan lifespan prediction using NASA N-CMAPSS data, offering a new perspective on the evolving dynamics of mean residual life and remaining useful life.