极值、左模性和半分布性

IF 0.6 4区数学 Q3 MATHEMATICS

Algebra Universalis Pub Date : 2023-04-17 DOI:10.1007/s00012-023-00814-8

Henri Mühle

{"title":"极值、左模性和半分布性","authors":"Henri Mühle","doi":"10.1007/s00012-023-00814-8","DOIUrl":null,"url":null,"abstract":"<div><p>In this article we study the relations between three classes of lattices each extending the class of distributive lattices in a different way. In particular, we consider join-semidistributive, join-extremal and left-modular lattices, respectively. Our main motivation is a recent result by Thomas and Williams proving that every semidistributive, extremal lattice is left modular. We prove the converse of this on a slightly more general level. Our main result asserts that every join-semidistributive, left-modular lattice is join extremal. We also relate these properties to the topological notion of lexicographic shellability.</p></div>","PeriodicalId":50827,"journal":{"name":"Algebra Universalis","volume":null,"pages":null},"PeriodicalIF":0.6000,"publicationDate":"2023-04-17","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://link.springer.com/content/pdf/10.1007/s00012-023-00814-8.pdf","citationCount":"1","resultStr":"{\"title\":\"Extremality, left-modularity and semidistributivity\",\"authors\":\"Henri Mühle\",\"doi\":\"10.1007/s00012-023-00814-8\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>In this article we study the relations between three classes of lattices each extending the class of distributive lattices in a different way. In particular, we consider join-semidistributive, join-extremal and left-modular lattices, respectively. Our main motivation is a recent result by Thomas and Williams proving that every semidistributive, extremal lattice is left modular. We prove the converse of this on a slightly more general level. Our main result asserts that every join-semidistributive, left-modular lattice is join extremal. We also relate these properties to the topological notion of lexicographic shellability.</p></div>\",\"PeriodicalId\":50827,\"journal\":{\"name\":\"Algebra Universalis\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2023-04-17\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://link.springer.com/content/pdf/10.1007/s00012-023-00814-8.pdf\",\"citationCount\":\"1\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Algebra Universalis\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00012-023-00814-8\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Algebra Universalis","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s00012-023-00814-8","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 1

摘要

在本文中，我们研究了三类格之间的关系，每类格都以不同的方式扩展了分配格类。特别地，我们分别考虑连接半分布格、连接极值格和左模格。我们的主要动机是Thomas和Williams最近的一个结果，证明了每个半分布的极值格都是左模的。我们在稍微更一般的层面上证明了这一点的相反。我们的主要结果断言，每一个连接半分布左模格都是连接极值。我们还将这些性质与词典可壳性的拓扑概念联系起来。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

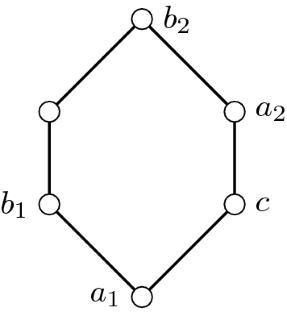
Extremality, left-modularity and semidistributivity

查看原文本刊更多论文

Extremality, left-modularity and semidistributivity

In this article we study the relations between three classes of lattices each extending the class of distributive lattices in a different way. In particular, we consider join-semidistributive, join-extremal and left-modular lattices, respectively. Our main motivation is a recent result by Thomas and Williams proving that every semidistributive, extremal lattice is left modular. We prove the converse of this on a slightly more general level. Our main result asserts that every join-semidistributive, left-modular lattice is join extremal. We also relate these properties to the topological notion of lexicographic shellability.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Algebra Universalis 数学-数学

CiteScore

1.00

自引率

16.70%

发文量

审稿时长

3 months

期刊介绍： Algebra Universalis publishes papers in universal algebra, lattice theory, and related fields. In a pragmatic way, one could define the areas of interest of the journal as the union of the areas of interest of the members of the Editorial Board. In addition to research papers, we are also interested in publishing high quality survey articles.