VTC 0$\mathsf｛VTC^0｝$作为指数整数部分的模型

IF 0.4 4区数学 Q4 LOGIC

Mathematical Logic Quarterly Pub Date : 2023-08-02 DOI:10.1002/malq.202300001

Emil Jeřábek

{"title":"VTC 0$\\mathsf｛VTC^0｝$作为指数整数部分的模型","authors":"Emil Jeřábek","doi":"10.1002/malq.202300001","DOIUrl":null,"url":null,"abstract":"<p>We prove that (additive) ordered group reducts of nonstandard models of the bounded arithmetical theory <math>\n <semantics>\n <msup>\n <mi>VTC</mi>\n <mn>0</mn>\n </msup>\n <annotation>$\\mathsf {VTC^0}$</annotation>\n </semantics></math> are recursively saturated in a rich language with predicates expressing the integers, rationals, and logarithmically bounded numbers. Combined with our previous results on the construction of the real exponential function on completions of models of <math>\n <semantics>\n <msup>\n <mi>VTC</mi>\n <mn>0</mn>\n </msup>\n <annotation>$\\mathsf {VTC^0}$</annotation>\n </semantics></math>, we show that every countable model of <math>\n <semantics>\n <msup>\n <mi>VTC</mi>\n <mn>0</mn>\n </msup>\n <annotation>$\\mathsf {VTC^0}$</annotation>\n </semantics></math> is an exponential integer part of a real-closed exponential field.</p>","PeriodicalId":49864,"journal":{"name":"Mathematical Logic Quarterly","volume":"69 2","pages":"244-260"},"PeriodicalIF":0.4000,"publicationDate":"2023-08-02","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1002/malq.202300001","citationCount":"1","resultStr":"{\"title\":\"Models of \\n \\n \\n VTC\\n 0\\n \\n $\\\\mathsf {VTC^0}$\\n as exponential integer parts\",\"authors\":\"Emil Jeřábek\",\"doi\":\"10.1002/malq.202300001\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>We prove that (additive) ordered group reducts of nonstandard models of the bounded arithmetical theory <math>\\n <semantics>\\n <msup>\\n <mi>VTC</mi>\\n <mn>0</mn>\\n </msup>\\n <annotation>$\\\\mathsf {VTC^0}$</annotation>\\n </semantics></math> are recursively saturated in a rich language with predicates expressing the integers, rationals, and logarithmically bounded numbers. Combined with our previous results on the construction of the real exponential function on completions of models of <math>\\n <semantics>\\n <msup>\\n <mi>VTC</mi>\\n <mn>0</mn>\\n </msup>\\n <annotation>$\\\\mathsf {VTC^0}$</annotation>\\n </semantics></math>, we show that every countable model of <math>\\n <semantics>\\n <msup>\\n <mi>VTC</mi>\\n <mn>0</mn>\\n </msup>\\n <annotation>$\\\\mathsf {VTC^0}$</annotation>\\n </semantics></math> is an exponential integer part of a real-closed exponential field.</p>\",\"PeriodicalId\":49864,\"journal\":{\"name\":\"Mathematical Logic Quarterly\",\"volume\":\"69 2\",\"pages\":\"244-260\"},\"PeriodicalIF\":0.4000,\"publicationDate\":\"2023-08-02\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1002/malq.202300001\",\"citationCount\":\"1\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Mathematical Logic Quarterly\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1002/malq.202300001\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"LOGIC\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Mathematical Logic Quarterly","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1002/malq.202300001","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"LOGIC","Score":null,"Total":0}

引用次数: 1

摘要

我们证明了有界算术理论VTC0$\mathsf{VTC^0}$的非标准模型的（加性）有序群约简在一种丰富的语言中递归饱和，该语言中谓词表示整数、有理数和对数有界数。结合我们以前关于VTC0$\mathsf{VTC^0}$模型完备的实指数函数构造的结果，我们证明了VTC0$\mathsf{VTC^0}$的每个可数模型都是实闭指数域的指数整数部分。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

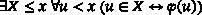
$Models of VTC 0 $\mathsf {VTC^0}$ as exponential integer parts$

查看原文本刊更多论文

Models of VTC 0 $\mathsf {VTC^0}$ as exponential integer parts

We prove that (additive) ordered group reducts of nonstandard models of the bounded arithmetical theory ${VTC}^{0}$ are recursively saturated in a rich language with predicates expressing the integers, rationals, and logarithmically bounded numbers. Combined with our previous results on the construction of the real exponential function on completions of models of ${VTC}^{0}$ , we show that every countable model of ${VTC}^{0}$ is an exponential integer part of a real-closed exponential field.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Mathematical Logic Quarterly 数学-数学

CiteScore

0.60

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： Mathematical Logic Quarterly publishes original contributions on mathematical logic and foundations of mathematics and related areas, such as general logic, model theory, recursion theory, set theory, proof theory and constructive mathematics, algebraic logic, nonstandard models, and logical aspects of theoretical computer science.