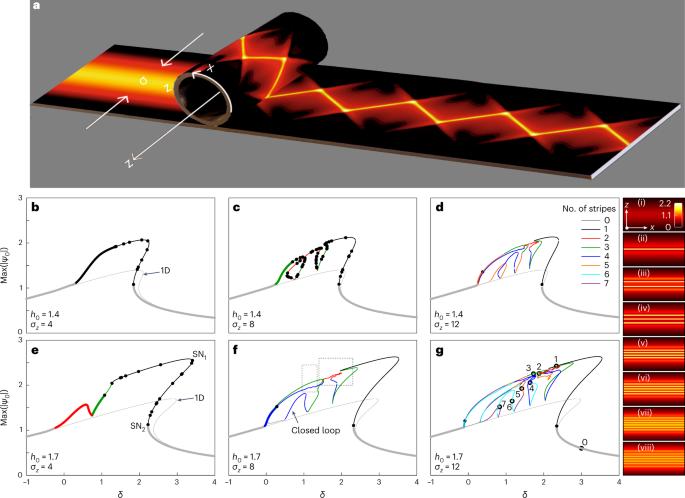
Photonic snake states in two-dimensional frequency combs

Taming the instabilities inherent to many nonlinear optical phenomena is of paramount importance for modern photonics. In particular, the so-called snake instability is universally known to severely distort localized wave stripes, leading to the occurrence of transient, short-lived dynamical states that eventually decay. This phenomenon is ubiquitous in nonlinear science—from river meandering to superfluids—and so far it apparently remains uncontrollable; however, here we show that optical snake instabilities can be harnessed by a process that leads to the formation of stationary and robust two-dimensional zigzag states. We find that such a new type of nonlinear waves exists in the hyperbolic regime of cylindrical microresonators, and that it naturally corresponds to two-dimensional frequency combs featuring spectral heterogeneity and intrinsic synchronization. We uncover the conditions of the existence of such spatiotemporal photonic snakes and confirm their remarkable robustness against perturbations. Our findings represent a new paradigm for frequency comb generation, thus opening the door to a whole range of applications in communications, metrology and spectroscopy. By tuning the spatial width, the strength and the frequency of a pump beam in two-dimensional cylindrical microcavities supporting stable, robust photonic snake states, a set of broadband and perfectly synchronized two-dimensional frequency combs can be realized.