一般代数的弱Schreier扩张
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
弱Schreier分裂扩张是一类相当大但被很好地理解的单拟扩张,它推广了群的分裂扩张的一些方面。这个简短的注释提供了一种定义和研究一般代数结构中类似的分裂扩展类的方法(用术语\(\θ\)参数化)。这些推广了拟单群的弱Schreier扩展,以及半阿贝尔变体的一般扩展(使用在其句法表征中出现的\(\theta\))。再次限制在半群的情况下,对\(θ)的不同选择导致了一类新的半群扩展,比弱Schreier分裂扩展更普遍。本文章由计算机程序翻译,如有差异,请以英文原文为准。
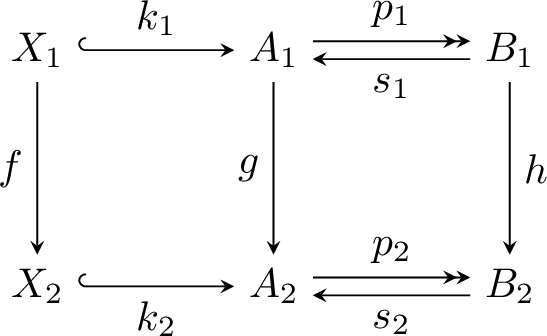
Weakly Schreier extensions for general algebras
Weakly Schreier split extensions are a reasonably large, yet well-understood class of monoid extensions, which generalise some aspects of split extensions of groups. This short note provides a way to define and study similar classes of split extensions in general algebraic structures (parameterised by a term \(\theta \)). These generalise weakly Schreier extensions of monoids, as well as general extensions of semi-abelian varieties (using the \(\theta \) appearing in their syntactic characterisation). Restricting again to the case of monoids, a different choice of \(\theta \) leads to a new class of monoid extensions, more general than the weakly Schreier split extensions.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Algebra Universalis
数学-数学
CiteScore
1.00
自引率
16.70%
发文量
34
审稿时长
3 months
期刊介绍:
Algebra Universalis publishes papers in universal algebra, lattice theory, and related fields. In a pragmatic way, one could define the areas of interest of the journal as the union of the areas of interest of the members of the Editorial Board. In addition to research papers, we are also interested in publishing high quality survey articles.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


