辛的帽子

IF 0.8 2区数学 Q2 MATHEMATICS

Journal of Topology Pub Date : 2022-10-12 DOI:10.1112/topo.12258

John B. Etnyre, Marco Golla

{"title":"辛的帽子","authors":"John B. Etnyre, Marco Golla","doi":"10.1112/topo.12258","DOIUrl":null,"url":null,"abstract":"<p>We study relative symplectic cobordisms between contact submanifolds, and in particular relative symplectic cobordisms to the empty set, that we call hats. While we make some observations in higher dimensions, we focus on the case of transverse knots in the standard 3-sphere, and hats in blow-ups of the (punctured) complex projective planes. We apply the construction to give constraints on the algebraic topology of fillings of double covers of the 3-sphere branched over certain transverse quasipositive knots.</p>","PeriodicalId":56114,"journal":{"name":"Journal of Topology","volume":"15 4","pages":"2216-2269"},"PeriodicalIF":0.8000,"publicationDate":"2022-10-12","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://londmathsoc.onlinelibrary.wiley.com/doi/epdf/10.1112/topo.12258","citationCount":"6","resultStr":"{\"title\":\"Symplectic hats\",\"authors\":\"John B. Etnyre, Marco Golla\",\"doi\":\"10.1112/topo.12258\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>We study relative symplectic cobordisms between contact submanifolds, and in particular relative symplectic cobordisms to the empty set, that we call hats. While we make some observations in higher dimensions, we focus on the case of transverse knots in the standard 3-sphere, and hats in blow-ups of the (punctured) complex projective planes. We apply the construction to give constraints on the algebraic topology of fillings of double covers of the 3-sphere branched over certain transverse quasipositive knots.</p>\",\"PeriodicalId\":56114,\"journal\":{\"name\":\"Journal of Topology\",\"volume\":\"15 4\",\"pages\":\"2216-2269\"},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2022-10-12\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://londmathsoc.onlinelibrary.wiley.com/doi/epdf/10.1112/topo.12258\",\"citationCount\":\"6\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Topology\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1112/topo.12258\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Topology","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/topo.12258","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 6

摘要

我们研究了接触子流形之间的相对辛协，特别是空集的相对辛协，我们称之为帽。虽然我们在更高的维度上进行了一些观察，但我们关注的是标准3球中的横向结，以及(穿孔)复杂投影平面的放大图。我们应用该构造给出了分支于某些横向拟正结上的3球的双复盖填充的代数拓扑的约束。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

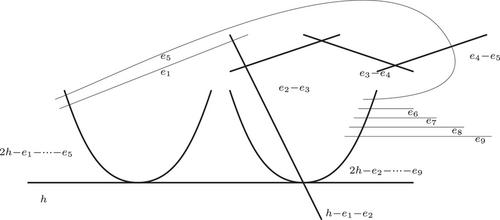
Symplectic hats

查看原文本刊更多论文

Symplectic hats

We study relative symplectic cobordisms between contact submanifolds, and in particular relative symplectic cobordisms to the empty set, that we call hats. While we make some observations in higher dimensions, we focus on the case of transverse knots in the standard 3-sphere, and hats in blow-ups of the (punctured) complex projective planes. We apply the construction to give constraints on the algebraic topology of fillings of double covers of the 3-sphere branched over certain transverse quasipositive knots.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Topology 数学-数学

CiteScore

2.00

自引率

9.10%

发文量

审稿时长

>12 weeks

期刊介绍： The Journal of Topology publishes papers of high quality and significance in topology, geometry and adjacent areas of mathematics. Interesting, important and often unexpected links connect topology and geometry with many other parts of mathematics, and the editors welcome submissions on exciting new advances concerning such links, as well as those in the core subject areas of the journal. The Journal of Topology was founded in 2008. It is published quarterly with articles published individually online prior to appearing in a printed issue.