高阶Bernstein-Kantorovich算子
IF 0.8
4区 综合性期刊
Q3 MULTIDISCIPLINARY SCIENCES
Proceedings of the National Academy of Sciences, India Section A: Physical Sciences
Pub Date : 2023-01-18
DOI:10.1007/s40010-022-00804-w
引用次数: 1
摘要
在本文中,我们考虑与Bernstein多项式相关的高阶(j阶,\(j\in \textbf{N}_{0}\)) Bernstein - kantorovich算子。我们估计了一些直接结果,包括voronovskaja型渐近公式、同时逼近和误差估计。最后,通过图形表示进行了对比研究,并对误差值的上界进行了数值解释。本文章由计算机程序翻译,如有差异,请以英文原文为准。
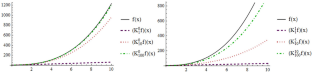
Higher-Order Bernstein–Kantorovich Operators
In the present paper, we consider the higher-order (j-th order, \(j\in \textbf{N}_{0}\)) Bernstein–Kantorovich operators, which are connected with the Bernstein polynomials. We estimate some direct results including the Voronovskaja-kind asymptotic formula, simultaneous approximation and error estimations. In the end, we present comparative study through graphical representation and numerically interpret the upper bound of the error value.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
2.60
自引率
0.00%
发文量
37
审稿时长
>12 weeks
期刊介绍:
To promote research in all the branches of Science & Technology; and disseminate the knowledge and advancements in Science & Technology

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


