具有时变参数的扩散模型:不同数值方法的计算量和精度分析
IF 1.5
4区 心理学
Q2 MATHEMATICS, INTERDISCIPLINARY APPLICATIONS
引用次数: 3
摘要
漂移扩散模型已经成为当代心理学和神经科学许多领域的宝贵工具。本研究比较和分析了不同的方法(即随机微分方程、积分法、Kolmogorov方程和矩阵法)来推导这些模型预测的首次通过时间分布。首先,对这些方法的准确性和效率进行了比较。特别是,我们解决了非标准问题,例如,具有时间相关漂移率或时间相关阈值的模型。其次,对这些方法进行了数学分析和分类。最后,我们讨论它们的优势和注意事项。本文章由计算机程序翻译,如有差异,请以英文原文为准。
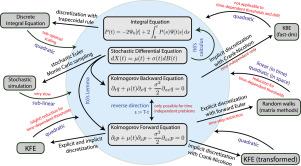
Diffusion models with time-dependent parameters: An analysis of computational effort and accuracy of different numerical methods
Drift-diffusion models have become valuable tools in many fields of contemporary psychology and the neurosciences. The present study compares and analyzes different methods (i.e., stochastic differential equation, integral method, Kolmogorov equations, and matrix method) to derive the first-passage time distribution predicted by these models. First, these methods are compared in their accuracy and efficiency. In particular, we address non-standard problems, for example, models with time-dependent drift rates or time-dependent thresholds. Second, a mathematical analysis and a classification of these methods is provided. Finally, we discuss their strengths and caveats.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Journal of Mathematical Psychology
医学-数学跨学科应用
CiteScore
3.70
自引率
11.10%
发文量
37
审稿时长
20.2 weeks
期刊介绍:
The Journal of Mathematical Psychology includes articles, monographs and reviews, notes and commentaries, and book reviews in all areas of mathematical psychology. Empirical and theoretical contributions are equally welcome.
Areas of special interest include, but are not limited to, fundamental measurement and psychological process models, such as those based upon neural network or information processing concepts. A partial listing of substantive areas covered include sensation and perception, psychophysics, learning and memory, problem solving, judgment and decision-making, and motivation.
The Journal of Mathematical Psychology is affiliated with the Society for Mathematical Psychology.
Research Areas include:
• Models for sensation and perception, learning, memory and thinking
• Fundamental measurement and scaling
• Decision making
• Neural modeling and networks
• Psychophysics and signal detection
• Neuropsychological theories
• Psycholinguistics
• Motivational dynamics
• Animal behavior
• Psychometric theory
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


