从静态三维麦克斯韦-陈-西蒙斯电磁学产生杰基-泰特尔伯姆欧几里得引力
IF 4.6
2区 物理与天体物理
Q1 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
摘要
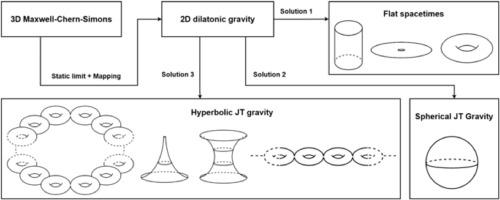
我们考虑纯三维麦克斯韦-陈-西蒙斯电动力学的静态极限。我们证明了这一理论可以映射到一个二维引力模型上,该模型是具有欧几里得特征的黎曼流形的一阶形式,耦合到一个自然地被解释为膨胀的实标量场。在这个框架中,二维的牛顿常数和宇宙学常数完全由电荷决定。这个引力模型的解被发现是平凡的:一个平坦流形上的常数膨胀场。然而,我们引入了自旋连接的两个不同的位移,将模型转换为Jackiw-Teitelboim引力。具体地说,我们确定了两个附加解:一个双曲流形也具有常数膨胀构型;在球面流形中,膨胀假设为常数,非零场构型。在这两种非平坦情况下,通过在紧流形的特殊情况下应用高斯-邦尼特定理,我们建立了流形的半径是由宇宙学常数固定的(因此,由电荷固定)。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Generating Jackiw-Teitelboim Euclidean gravity from static three-dimensional Maxwell-Chern-Simons electromagnetism
We consider pure three-dimensional Maxwell-Chern-Simons electrodynamics in the static limit. We show that this theory can be mapped onto a two-dimensional gravitational model in the first-order formalism of Riemannian manifolds with Euclidean signature, coupled to a real scalar field naturally interpreted as a dilaton. In this framework, the Newtonian and cosmological constants in two dimensions are fully determined by the electric charge. The solution to this gravitational model is found to be trivial: a constant dilaton field on a flat manifold. However, we introduce two distinct shifts of the spin connection that transform the model into Jackiw-Teitelboim gravity. Specifically, we identify two additional solutions: a hyperbolic manifold with also a constant dilaton configuration; and a spherical manifold where, again, the dilaton assumes a constant, nonzero field configuration. In both non-flat cases, by employing the Gauss-Bonnet theorem in the specific cases of compact manifolds, we establish that the manifold’s radius is fixed by the cosmological constant (and, therefore, by the electric charge).
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Chinese Journal of Physics
物理-物理:综合
CiteScore
8.50
自引率
10.00%
发文量
361
审稿时长
44 days
期刊介绍:
The Chinese Journal of Physics publishes important advances in various branches in physics, including statistical and biophysical physics, condensed matter physics, atomic/molecular physics, optics, particle physics and nuclear physics.
The editors welcome manuscripts on:
-General Physics: Statistical and Quantum Mechanics, etc.-
Gravitation and Astrophysics-
Elementary Particles and Fields-
Nuclear Physics-
Atomic, Molecular, and Optical Physics-
Quantum Information and Quantum Computation-
Fluid Dynamics, Nonlinear Dynamics, Chaos, and Complex Networks-
Plasma and Beam Physics-
Condensed Matter: Structure, etc.-
Condensed Matter: Electronic Properties, etc.-
Polymer, Soft Matter, Biological, and Interdisciplinary Physics.
CJP publishes regular research papers, feature articles and review papers.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


