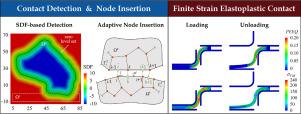
A virtual element framework for inelastic contact involving multiple bodies

The Virtual Element Method (VEM) is a recently developed technique well-suited for arbitrary cell shapes, converting non-conformal meshes into node-to-node constraint enforcement through adaptive node insertion. Despite this advantage, computational contact mechanics including VEM approaches still presents significant challenges, particularly when dealing with arbitrary geometries, finite deformations, material non-linearity, and friction. In this study, we develop a VEM framework aided by the signed distance function (SDF), which provides an efficient geometric representation for gap measurements and facilitates adaptive node insertion. Leveraging automatic differentiation, we further extend the method to handle contacts involving elasto-plastic finite deformation within an energy-based framework. The contact contribution including both normal and frictional effects, is efficiently computed using a finite difference approximation of the stiffness matrix. Through comprehensive numerical benchmarks including Hertzian contact problems, we validate the accuracy of the proposed approach under small and finite deformations, with and without plasticity. Additionally, we demonstrate the method’s effectiveness in multi-body contact scenarios and a deep drawing process simulation. The results indicate that the SDF-based VEM framework is a reliable and versatile tool for solving challenging contact problems.