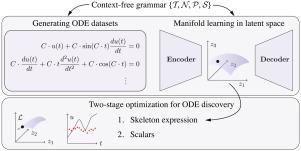
Grammar-based ordinary differential equation discovery

The understanding and modeling of complex physical phenomena through dynamical systems has historically driven scientific progress, providing essential tools for predicting system behavior under diverse conditions over time. In engineering, the discovery of dynamical systems is indispensable for computational modeling, diagnostics, prognostics, and control of engineered systems. Joining recent efforts that harness the power of symbolic regression in this domain, we propose a novel framework for the end-to-end discovery of ordinary differential equations (ODEs), termed Grammar-based ODE Discovery Engine (GODE). The proposed methodology combines formal grammars with dimensionality reduction and stochastic search for efficiently navigating high-dimensional combinatorial spaces. Grammars serve to inject domain knowledge and provide structure, both constraining and guiding the search for candidate expressions. GODE proves to be more sample- and parameter-efficient than state-of-the-art transformer-based models and to discover more accurate and parsimonious ODE expressions than both genetic programming- and other grammar-based methods, particularly for complex inference tasks, such as the discovery of structural dynamics. Thus, we introduce a tool that could play a catalytic role in dynamics discovery tasks, including modeling, system identification, and monitoring applications.