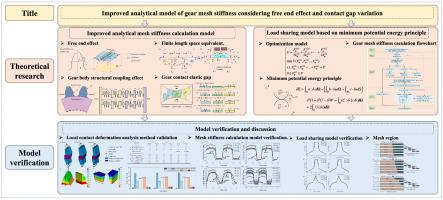
Improved analytical model of gear mesh stiffness considering free end effect and contact gap variation

In gear systems, mesh stiffness is regarded as a significant internal excitation with critical influences on the gear dynamics. The existing analytical model for mesh stiffness calculation determines contact stiffness without accounting for stress concentration at the free end, and it neglects variations in the contacting gap when establishing the meshing interval for single and double teeth, resulting in calculation inaccuracies. This paper proposes an analytical method(AM) to achieve highly efficient and precise calculations by considering free end effect and contact gap variation. The method developed correction coefficients using the elastic quarter-space quick correction method, based on Hertz contact theory, half-space theory, and minimum potential energy principle. Hertz contact theory and half-space theory can precisely compute the local contact deformation at the midpoint of tooth width. The elastic quarter-space fast correction method effectively accounts for the free end effect in finite-length space, enabling accurate calculation of local contact stiffness. A mesh stiffness calculation model is built based on the method recommended, considering gear body structure coupling effect and elastic contact gap variation. The precision and efficiency of the proposed method(PM) are verified by finite element method (FEM) benchmarks and existing common methods.