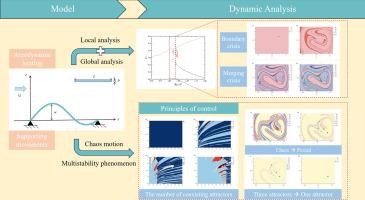
Global dynamics and multistability control of heated panel in supersonic flow

This study investigates the global dynamics of a heated, simply supported panel in supersonic flow with structural nonlinearity and support motion. The governing equations, derived using von Kármán’s large deflection theory and first-order piston theory, are discretized into ordinary differential equations via Galerkin’s method. Using the composite cell coordinate cystem (CCCS) method for global analysis, we identify that variations in excitation amplitude and thermal stress trigger three critical transitions: boundary, interior, and merging crises, inducing multistability with interlaced basins of attraction. The multistability property increases the system’s sensitivity to perturbations, threatening the panel’s safe service. To address this, we first established a mapping between excitation parameters and the number of coexisting attractors, and then presented a control strategy. Numerical simulation results show that the strategy successfully eliminates coexisting attractors and can even convert chaotic motion into periodic orbits. Our findings provide novel insights into the nonlinear dynamics of panels in supersonic flow and establish a theoretical basis for the control of multistability.