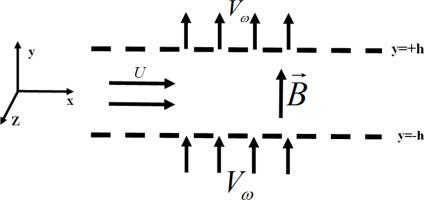
Stability analysis of viscoelastic Kelvin–Voigt fluid in anisotropic porous media in the presence of hydromagnetic, small suction and injection effect

The flow of fluids through porous media is fundamental to many scientific and engineering applications, including electrochromatography, micropumping systems, subsurface geological processes, polymer processing, and contaminated soil remediation. These systems often involve viscoelastic fluids such as polymer solutions, emulsions, suspensions, and biological fluids whose complex rheological properties significantly affect flow dynamics. This study offers a comprehensive linear stability analysis of a viscoelastic Kelvin–Voigt fluid flowing through an anisotropic porous medium under a uniform transverse magnetic field with boundary injection/suction effects. A modified Orr–Sommerfeld eigenvalue problem is derived using normal mode analysis and solved numerically via the Chebyshev spectral collocation method. The resulting profiles of perturbation growth rates, critical Reynolds numbers, and instability thresholds are systematically examined concerning key parameters, including the Kelvin–Voigt relaxation time, Darcy number, injection/suction Reynolds number, anisotropy coefficient, wavenumber, and Hartmann number. The analysis shows that higher Darcy and wave numbers stabilise the flow, while moderate injection/suction increases stability by raising the critical Reynolds number and delaying instability onset. The transverse magnetic field reduces flow disturbances through Lorentz force effects, decreasing kinetic energy and fostering laminar flow. Conversely, mechanical anisotropy enhances velocity fluctuations and destabilises the flow. These results deepen the understanding of stability mechanisms in viscoelastic media and are relevant for applications such as polymer extrusion, MHD transport, nuclear cooling systems, chemical reactors, and advanced manufacturing processes in aerospace and biomedical engineering.