具有多项式衰减步长的大象随机漫步
IF 1.2
3区 物理与天体物理
Q3 PHYSICS, MATHEMATICAL
引用次数: 0
摘要
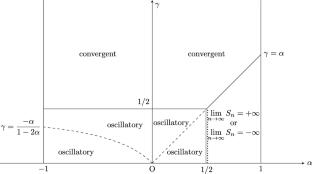
本文引入了步长呈多项式衰减的大象随机漫步的一种变体。在每个时刻k,步行者的步长为\(k^{-\gamma }\)与\(\gamma >0\)。我们研究步长指数\(\gamma \)和记忆参数\(\alpha \in [-1,1]\)对步行器长时间行为的影响。对于固定\(\alpha \),在\(\gamma _{c}(\alpha )=\max \{\alpha ,1/2\}\)处允许从发散到收敛(局部化)的相变。这意味着足够大的记忆效应可以改变定位的临界点。此外,我们还得到了一些定量极限定理,这些定理提供了行走器长时间行为的详细图像。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Elephant Random Walk with Polynomially Decaying Steps
In this paper, we introduce a variation of the elephant random walk whose steps are polynomially decaying. At each time k, the walker’s step size is \(k^{-\gamma }\) with \(\gamma >0\). We investigate effects of the step size exponent \(\gamma \) and the memory parameter \(\alpha \in [-1,1]\) on the long-time behavior of the walker. For fixed \(\alpha \), it admits phase transition from divergence to convergence (localization) at \(\gamma _{c}(\alpha )=\max \{\alpha ,1/2\}\). This means that large enough memory effect can shift the critical point for localization. Moreover, we obtain quantitative limit theorems which provide a detailed picture of the long-time behavior of the walker.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Journal of Statistical Physics
物理-物理:数学物理
CiteScore
3.10
自引率
12.50%
发文量
152
审稿时长
3-6 weeks
期刊介绍:
The Journal of Statistical Physics publishes original and invited review papers in all areas of statistical physics as well as in related fields concerned with collective phenomena in physical systems.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


