定向渗流模型临界值下界的更新

IF 1.2 3区物理与天体物理 Q3 PHYSICS, MATHEMATICAL

Journal of Statistical Physics Pub Date : 2025-06-11 DOI:10.1007/s10955-025-03466-1

Olivier Couronné

{"title":"定向渗流模型临界值下界的更新","authors":"Olivier Couronné","doi":"10.1007/s10955-025-03466-1","DOIUrl":null,"url":null,"abstract":"<div><p>We obtain new lower bounds on the critical points for various models of oriented percolation. The method relies on establishing a stochastic domination of the percolation processes by multitype Galton-Watson trees. This approach can be applied to classical bond and site oriented percolation on <span>\\(\\mathbb {Z}^2\\)</span>, as well as to other lattices, such as inhomogeneous ones, and in three dimensions.</p></div>","PeriodicalId":667,"journal":{"name":"Journal of Statistical Physics","volume":"192 6","pages":""},"PeriodicalIF":1.2000,"publicationDate":"2025-06-11","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"An Update on Lower Bounds for the Critical Values of Oriented Percolation Models\",\"authors\":\"Olivier Couronné\",\"doi\":\"10.1007/s10955-025-03466-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We obtain new lower bounds on the critical points for various models of oriented percolation. The method relies on establishing a stochastic domination of the percolation processes by multitype Galton-Watson trees. This approach can be applied to classical bond and site oriented percolation on <span>\\\\(\\\\mathbb {Z}^2\\\\)</span>, as well as to other lattices, such as inhomogeneous ones, and in three dimensions.</p></div>\",\"PeriodicalId\":667,\"journal\":{\"name\":\"Journal of Statistical Physics\",\"volume\":\"192 6\",\"pages\":\"\"},\"PeriodicalIF\":1.2000,\"publicationDate\":\"2025-06-11\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Statistical Physics\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s10955-025-03466-1\",\"RegionNum\":3,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"PHYSICS, MATHEMATICAL\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Statistical Physics","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.1007/s10955-025-03466-1","RegionNum":3,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"PHYSICS, MATHEMATICAL","Score":null,"Total":0}

引用次数: 0

摘要

我们得到了各种定向渗流模型的临界点的新下界。该方法依赖于建立多类型高尔顿-沃森树对渗透过程的随机控制。这种方法可以应用于\(\mathbb {Z}^2\)上的经典键和面向位置的渗透，以及其他晶格，如非均匀晶格和三维晶格。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

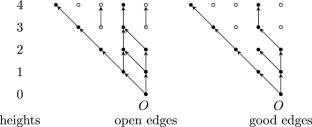
An Update on Lower Bounds for the Critical Values of Oriented Percolation Models

查看原文本刊更多论文

An Update on Lower Bounds for the Critical Values of Oriented Percolation Models

We obtain new lower bounds on the critical points for various models of oriented percolation. The method relies on establishing a stochastic domination of the percolation processes by multitype Galton-Watson trees. This approach can be applied to classical bond and site oriented percolation on \(\mathbb {Z}^2\), as well as to other lattices, such as inhomogeneous ones, and in three dimensions.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Statistical Physics 物理-物理：数学物理

CiteScore

3.10

自引率

12.50%

发文量

152

审稿时长

3-6 weeks

期刊介绍： The Journal of Statistical Physics publishes original and invited review papers in all areas of statistical physics as well as in related fields concerned with collective phenomena in physical systems.