经典海森堡模型的对称性
IF 0.5
4区 物理与天体物理
Q4 MECHANICS
引用次数: 0
摘要
研究了经典海森堡模型的对称性。证明了这种对称是共形变换和旋转的群。研究了涡旋结构对旋转群的不变性。将发现的场旋转群变换应用于先前发现的Heisenberg模型解(如瞬子,漩涡“目标”和“螺旋”)产生其他结构,这些结构也是该模型的解,其性质由原始结构决定。这也是该模型的解,具有由原始结构决定的性质。本文章由计算机程序翻译,如有差异,请以英文原文为准。
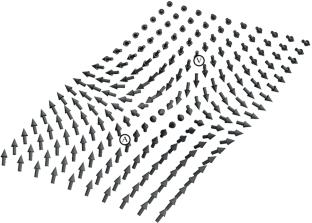
Symmetries of the Classical Heisenberg Model
The symmetries of the classical Heisenberg model are investigated. It is shown that such symmetries are groups of conformal transformations and rotations. The invariance of vortex structures with respect to the rotation group is studied. Application of the found transformations of the field rotation group to the previously found solutions of the Heisenberg model (such as instantons, vortex “targets” and “spirals”) generates other structures, which are also solutions to this model, the properties of which are determined by the original structures. which are also solutions of this model, with the properties determined by the original structures.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Doklady Physics
物理-力学
CiteScore
1.40
自引率
12.50%
发文量
12
审稿时长
4-8 weeks
期刊介绍:
Doklady Physics is a journal that publishes new research in physics of great significance. Initially the journal was a forum of the Russian Academy of Science and published only best contributions from Russia in the form of short articles. Now the journal welcomes submissions from any country in the English or Russian language. Every manuscript must be recommended by Russian or foreign members of the Russian Academy of Sciences.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


