内共振为1:2的分段线性齿轮传动系统的耦合模次谐波谐振
IF 8.9
1区 工程技术
Q1 ENGINEERING, MECHANICAL
引用次数: 0
摘要
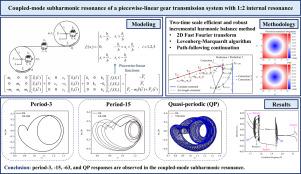
研究了内共振为1:2的分段线性齿轮传动系统的耦合模次谐波谐振。当系统以接近其第一和第三固有频率之和的频率激励时,两种模式同时被激活,产生周期3耦合模式响应。提出了一种计算分段线性齿轮传动系统周期响应的高效鲁棒增量谐波平衡(ER-IHB)方法,该方法具有显著提高计算效率和收敛性的特点,并对拟周期响应提出了其两时标变体——双时标高效鲁棒增量谐波平衡(TER-IHB)方法。采用快速傅里叶变换(FFT)和二维FFT分别对周期解和QP解的残差向量和雅可比矩阵进行高效求值,并采用Levenberg-Marquardt算法增强收敛性。此外,结合路径跟踪延拓技术计算响应曲线。采用提出的ER-IHB和TER-IHB方法对齿轮传动系统的幅频响应曲线进行了跟踪。对于周期解和QP解,所提方法的效率分别比传统的IHB方法高约2个数量级和4个数量级,并通过四阶龙格-库塔(RK)方法验证了其准确性。利用Floquet理论和扩展Floquet理论分别对周期解和QP解的稳定性进行了评价。识别出多个鞍节点和次级Hopf分岔,导致周期(周期-1、-3、-15和-63)、QP和混沌响应之间的转换。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Coupled-mode subharmonic resonance of a piecewise-linear gear transmission system with 1:2 internal resonance
The coupled-mode subharmonic resonance of a piecewise-linear gear transmission system with 1:2 internal resonance is investigated. When the system is excited at a frequency close to the sum of its first and third natural frequencies, both modes are simultaneously activated, giving rise to a period-3 coupled-mode response. An efficient and robust incremental harmonic balance (ER-IHB) method with significantly improved computational efficiency and convergence is developed for computing periodic responses of the piecewise-linear gear transmission system, and its two-time-scale variant, termed the two-time-scale efficient and robust incremental harmonic balance (TER-IHB) method, is formulated for quasi-periodic (QP) responses. Fast Fourier transform (FFT) and two-dimensional FFT are employed to efficiently evaluate the residual vectors and Jacobian matrices for periodic and QP solutions, respectively, and the Levenberg–Marquardt algorithm is utilized to enhance the convergence. Additionally, a path-following continuation technique is integrated to calculate response curves. The amplitude–frequency response curves of the gear transmission system are traced using the proposed ER-IHB and TER-IHB methods. The proposed methods are approximately two and four orders of magnitude more efficient than the conventional IHB method for periodic and QP solutions, respectively, and their accuracy is verified against the fourth-order Runge–Kutta (RK) method. Floquet and extended Floquet theories are employed to assess the stability of periodic and QP solutions, respectively. Multiple saddle–node and secondary Hopf bifurcations are identified, leading to transitions among periodic (period-1, -3, -15, and -63), QP, and chaotic responses.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Mechanical Systems and Signal Processing
工程技术-工程:机械
CiteScore
14.80
自引率
13.10%
发文量
1183
审稿时长
5.4 months
期刊介绍:
Journal Name: Mechanical Systems and Signal Processing (MSSP)
Interdisciplinary Focus:
Mechanical, Aerospace, and Civil Engineering
Purpose:Reporting scientific advancements of the highest quality
Arising from new techniques in sensing, instrumentation, signal processing, modelling, and control of dynamic systems
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


