增强各向同性板屈曲性能的刚度裁剪
IF 3.8
3区 工程技术
Q1 MECHANICS
International Journal of Solids and Structures
Pub Date : 2025-09-23
DOI:10.1016/j.ijsolstr.2025.113660
引用次数: 0
摘要
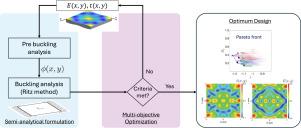
本研究研究了具有空间变化刚度分布的各向同性板的屈曲性能,通过三种设计策略:厚度变化、模量变化和组合方法来实现。基于经典板理论和瑞利-里兹法,建立了计算任意刚度型材临界屈曲载荷的半解析公式。为了探索设计空间,采用基于傅里叶的参数化进行了多目标优化,生成了能够捕捉屈曲能力和结构重量之间权衡的帕累托前沿。结果表明,与等质量的恒刚度设计相比,定制的刚度分布可以显著提高抗屈曲能力,最高可提高76%。在这些策略中,结合厚度-模量变化优于单独的方法,高阶傅立叶项可以更好地控制刚度梯度。通过有限元仿真验证了半解析模型,误差在5%以内,验证了模型的准确性。这项工作为通过空间刚度裁剪设计轻质、抗屈曲结构提供了计算框架和机械见解。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Stiffness tailoring for enhanced buckling performance of isotropic panels
This study investigates the buckling performance of isotropic panels with spatially varying stiffness distributions, achieved through three design strategies: thickness variation, modulus variation, and a combined approach. A semi-analytical formulation based on Classical Plate Theory and the Rayleigh–Ritz method was developed to compute critical buckling loads for arbitrary stiffness profiles. To explore the design space, multi-objective optimization was conducted using Fourier-based parameterization, producing Pareto fronts that capture the trade-off between buckling capacity and structural weight. Results show that tailored stiffness distributions can significantly improve buckling resistance—by up to 76%—compared to constant-stiffness designs of equal mass. Among the strategies, combined thickness–modulus variation outperformed individual approaches, and higher-order Fourier terms enabled finer control of stiffness gradients. The semi-analytical model was validated through finite element simulations, with discrepancies within 5%, confirming its accuracy. This work provides both a computational framework and mechanistic insights for designing lightweight, buckling-resistant structures via spatial stiffness tailoring.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
6.70
自引率
8.30%
发文量
405
审稿时长
70 days
期刊介绍:
The International Journal of Solids and Structures has as its objective the publication and dissemination of original research in Mechanics of Solids and Structures as a field of Applied Science and Engineering. It fosters thus the exchange of ideas among workers in different parts of the world and also among workers who emphasize different aspects of the foundations and applications of the field.
Standing as it does at the cross-roads of Materials Science, Life Sciences, Mathematics, Physics and Engineering Design, the Mechanics of Solids and Structures is experiencing considerable growth as a result of recent technological advances. The Journal, by providing an international medium of communication, is encouraging this growth and is encompassing all aspects of the field from the more classical problems of structural analysis to mechanics of solids continually interacting with other media and including fracture, flow, wave propagation, heat transfer, thermal effects in solids, optimum design methods, model analysis, structural topology and numerical techniques. Interest extends to both inorganic and organic solids and structures.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


