塑性变形作为相变:铜单晶塑性流动的组合模型
IF 6
2区 工程技术
Q2 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
摘要
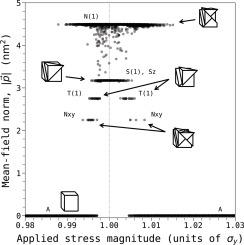
塑性连续统模型不能捕捉微观结构演化的丰富性,因为连续统是一种同质结构。目前的研究表明,在中尺度上,在真正离散的结构和离散的外部演算中,有一种替代方法是可用的。将已有的含两个参数的连续平均场模型用后者的语言重写,以模拟完美铜单晶在单轴拉伸作用下的塑性滑移事件网络的性质。采用Metropolis-Hastings算法在三维空间的二维三角形网格中模拟了系统的行为。不同性质的相出现,并观察到一阶和二阶相变。这些相代表了共线、共面、非共线和非共面主动滑移体系不同组合的塑性滑移网络排列。此外,这些相中的一些可以解释为代表晶体学现象,如二次滑移系统的激活,应变局部化和断裂或非晶化。一阶过渡主要作为外加应力的函数,而二阶过渡只作为平均场耦合参数的函数。前者让人想起其他统计力学模型中的过渡,而后者在实验观察中发现了相似之处。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Plastic deformation as a phase transition: A combinatorial model of plastic flow in copper single crystals
Continuum models of plasticity fail to capture the richness of microstructural evolution because the continuum is a homogeneous construction. The present study shows that an alternative way is available at the mesoscale in the form of truly discrete constructions and in the discrete exterior calculus. A pre-existing continuum mean-field model with two parameters is rewritten in the language of the latter to model the properties of a network of plastic slip events in a perfect copper single crystal under uniaxial tension. The behaviour of the system is simulated in a triangular 2D mesh in 3D space employing a Metropolis–Hastings algorithm. Phases of distinct character emerge and both first-order and second-order phase transitions are observed. The phases represent arrangements of the plastic slip network with different combinations of collinear, coplanar, non-collinear and non-coplanar active slip systems. Furthermore, some of these phases can be interpreted as representing crystallographic phenomena like activation of secondary slip systems, strain localisation and fracture or amorphisation. The first-order transitions mostly occur as functions of the applied stress, while the second-order transitions occur exclusively as functions of the mean-field coupling parameter. The former are reminiscent of transitions in other statistical–mechanical models, while the latter find parallels in experimental observations.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
9.80
自引率
9.40%
发文量
276
审稿时长
52 days
期刊介绍:
The aim of Journal of The Mechanics and Physics of Solids is to publish research of the highest quality and of lasting significance on the mechanics of solids. The scope is broad, from fundamental concepts in mechanics to the analysis of novel phenomena and applications. Solids are interpreted broadly to include both hard and soft materials as well as natural and synthetic structures. The approach can be theoretical, experimental or computational.This research activity sits within engineering science and the allied areas of applied mathematics, materials science, bio-mechanics, applied physics, and geophysics.
The Journal was founded in 1952 by Rodney Hill, who was its Editor-in-Chief until 1968. The topics of interest to the Journal evolve with developments in the subject but its basic ethos remains the same: to publish research of the highest quality relating to the mechanics of solids. Thus, emphasis is placed on the development of fundamental concepts of mechanics and novel applications of these concepts based on theoretical, experimental or computational approaches, drawing upon the various branches of engineering science and the allied areas within applied mathematics, materials science, structural engineering, applied physics, and geophysics.
The main purpose of the Journal is to foster scientific understanding of the processes of deformation and mechanical failure of all solid materials, both technological and natural, and the connections between these processes and their underlying physical mechanisms. In this sense, the content of the Journal should reflect the current state of the discipline in analysis, experimental observation, and numerical simulation. In the interest of achieving this goal, authors are encouraged to consider the significance of their contributions for the field of mechanics and the implications of their results, in addition to describing the details of their work.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


