面向增材制造的非均质晶格结构应力约束拓扑优化
IF 7.9
2区 材料科学
Q1 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
摘要
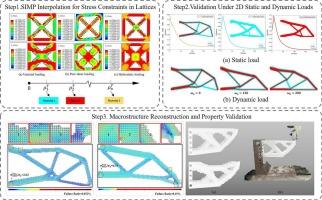
提出了一种受应力约束的非均相晶格结构拓扑优化方法。提出的方法扩展了有序的SIMP(固体各向同性材料与惩罚)框架,以纳入复合材料的失效准则。具体而言,采用改进的Tsai-Hill屈服准则来表征非均质晶格的各向异性屈服行为,随后将其作为应力约束集成到优化中。为了解决在不同晶格结构中屈服强度的变化,对应力场采用了一种归一化策略。此外,引入p -范数聚合方案,在有效处理局部应力约束的同时降低了计算成本。利用基于均质化理论的代表性体积元(RVE),得到了各晶格构型的等效弹性张量和屈服强度。通过一系列二维算例验证了该方法的有效性,实现了满足应力约束的轻量化结构设计。最后通过全尺寸力学分析和3D打印实验验证,进一步验证了优化结果的强度增强效果。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Stress-constrained topology optimization of heterogeneous lattice structures for additive manufacturing
This study presents a topology optimization method for heterogeneous lattice structures subject to stress constraints. The proposed approach extends the ordered SIMP (Solid Isotropic Material with Penalization) framework to incorporate a composite material failure criterion. Specifically, a modified Tsai–Hill yield criterion is employed to characterize the anisotropic yielding behavior of the heterogeneous lattice, which is subsequently integrated into the optimization as a stress constraint. To address the variation in yield strength across different lattice configurations, a normalization strategy is applied to the stress field. Additionally, a P-norm aggregation scheme is introduced to efficiently handle local stress constraints while reducing computational cost. The equivalent elastic tensor and yield strength of each lattice configuration are obtained using a representative volume element (RVE) based on homogenization theory. The effectiveness of the proposed method is demonstrated through a series of 2D cases, achieving lightweight structural designs that satisfy stress constraints. Finally, full-scale mechanical analysis and 3D printing experimental validation further confirm the strength reinforcement of the optimized results.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
Materials & Design
Engineering-Mechanical Engineering
CiteScore
14.30
自引率
7.10%
发文量
1028
审稿时长
85 days
期刊介绍:
Materials and Design is a multi-disciplinary journal that publishes original research reports, review articles, and express communications. The journal focuses on studying the structure and properties of inorganic and organic materials, advancements in synthesis, processing, characterization, and testing, the design of materials and engineering systems, and their applications in technology. It aims to bring together various aspects of materials science, engineering, physics, and chemistry.
The journal explores themes ranging from materials to design and aims to reveal the connections between natural and artificial materials, as well as experiment and modeling. Manuscripts submitted to Materials and Design should contain elements of discovery and surprise, as they often contribute new insights into the architecture and function of matter.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


