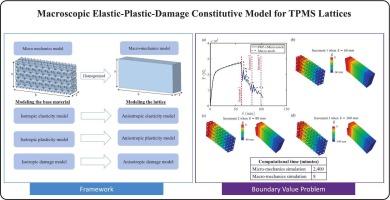
Macroscopic elastic-plastic-damage constitutive model for TPMS lattices

Lattices based on triply periodic minimal surfaces (TPMS), which are a class of architected cellular materials, have attracted significant attention lately, due to their prevailing multifunctional properties and due to the advancements in additive manufacturing technologies. However, TPMS lattices are computationally expensive to model explicitly when used in latticing various structures for enhanced mechanical properties. This study presents for the first time a macroscopic constitutive model that can predict the bulk anisotropic elastic–plastic-damage response of TPMS sheet-based lattices, including its numerical implementation using the finite element method. The proposed macroscopic constitutive model consists of a cubic symmetric elasticity model, a modified version of anisotropic Hill’s plasticity yield surface with an associative flow rule, and an anisotropic damage model such that both the plasticity and damage models account for the asymmetric behavior of lattices under tension and compression loading conditions. The developed macroscopic constitutive modeling is validated through predicting the elastic–plastic-damage behavior of the Schoen’s I-WP sheet-based TPMS lattice (IWP-s) at 28% relative density and Neovius sheet-based TPMS lattice (NEOV-s) at 25% relative density under various multi-axial loading conditions, where a very good match is obtained between the macroscopic models and the explicit micro-mechanics models of the lattices. In addition, validation is done on a cantilever beam problem that consists of homogenous distributions of TPMS sheet-based lattices where a very good match is found between the latticed beam’s elastic and elastic–plastic-damage responses and the macroscopic models’ predictions for both IWP-s and NEOV-s, while saving about 2778 times the computational time. This macroscopic continuum modeling framework helps in the development of computationally effective coupled elastic–plastic-damage constitutive models for various types of lattice metamaterials.