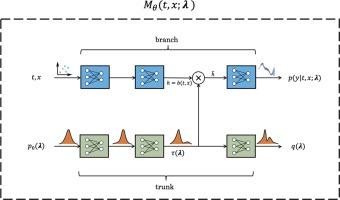
Deep operator networks for Bayesian parameter estimation in PDEs

We present a novel framework combining Deep Operator Networks (DeepONets) with Physics-Informed Neural Networks (PINNs) to solve partial differential equations (PDEs) while estimating their unknown parameters. By integrating data-driven learning with physical constraints, our method achieves robust and accurate solutions across diverse scenarios. Bayesian training is implemented through variational inference, allowing for comprehensive uncertainty quantification for both data and model uncertainties. This ensures reliable prediction and parameter estimates even in noisy conditions or when some of the physical equations governing the problem are missing. The framework demonstrates its efficacy in solving forward and inverse problems, including the 1D unsteady heat equation, 2D reaction-diffusion equations, 3D eigenvalue problem, and various regression tasks with sparse, noisy observations. This approach provides a computationally efficient and generalizable method for addressing uncertainty quantification in PDE surrogate modeling.