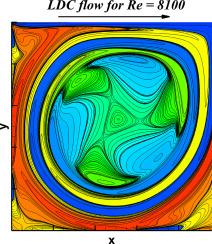
Benchmark study of unsteady flow inside a square lid driven cavity

The present work provides a time-resolved benchmark dataset for simulating supercritical, unsteady flow inside a square lid-driven cavity (LDC). To explain the role of fidelity of the computations and that of the numerical error in triggering instabilities, the flow is computed with three time-steps. This effort is substantiated with the use of an error dynamics equation, developed to model the physical processes in the Navier–Stokes equation (NSE), using global spectral analysis (GSA) of a model convection–diffusion equation. The error is found to be diffusion-dominated for this particular class of flows. There exists lack of consensus regarding the critical value of Reynolds number ($Re$) beyond which flow becomes unsteady for the square LDC. The study aims to bridge this gap by devoting a detailed discussion on the onset of unsteadiness by simulating LDC for $Re$ in the range of 7900 to 8900. Furthermore, the first Hopf bifurcation that is typically observed for LDC is quantified, laying the foundation for development of data-driven machine learning alternatives to expensive high fidelity simulations.