稳定层流流体通过基于圆渐开线的螺旋导管
IF 4.4
2区 工程技术
Q1 ENGINEERING, MULTIDISCIPLINARY
引用次数: 0
摘要
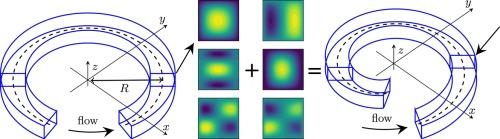
我们重新分析稳定层流不可压缩牛顿流体流过(平面)螺旋导管几何。螺旋导管被用于许多流体流动应用,主要是因为它们能够将大的流动距离纳入相对较小的体积。阿基米德螺旋是一个有吸引力的设计选择,在许多应用领域,包括微流体装置,由于其描述的简单性和一个恒定的间距。在这里,我们检查流体流动通过一个螺旋导管几何基于一个圆的渐开线。这些基于渐开线的螺旋管道几何形状保留了阿基米德螺旋的一些关键特征,同时拥有一些理想的设计特性。此外,围绕渐开线螺旋构建的曲线坐标系自然会导致直接的正交坐标系,这有助于详细分析流体流过螺旋导管的几何形状。我们利用这个坐标系推导了Navier-Stokes方程,并分析了流体在螺旋管道中的流动,重点是与轴对称弯曲管道的流动进行了详细的比较。我们的分析最终提供了一种估计螺旋管道流量的有效方法,为在某些情况下使用弯曲管道流量作为螺旋管道流量的近似提供了强有力的理由,并揭示了螺旋和轴对称弯曲管道之间的一些具体差异,而不会被曲率参数扰动所混淆。我们的方法很容易应用于研究任何横截面形状的螺旋风管,包括在各种应用中常见的矩形横截面。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Steady laminar fluid flow through spiral ducts based on circle involutes
We revisit the analysis of steady laminar incompressible Newtonian fluid flow through (planar) spiral duct geometries. Spiral ducts are utilised in a number of fluid flow applications, largely due to their ability to incorporate a large flow distance into a relatively small volume. Archimedean spirals are an attractive design choice in many application areas, including microfluidic devices, due to the simplicity of their description and a constant spacing between turns. Herein we examine fluid flow through a spiral duct geometry based on the involute of a circle. These involute based spiral duct geometries retain some key features of Archimedean spirals while possessing several desirable design properties. Moreover, a curvilinear coordinate system constructed around an involute spiral naturally leads to a straightforward orthogonal coordinate system which facilitates a detailed analysis of fluid flow through the spiral duct geometry. We derive the Navier–Stokes equations using this coordinate system and analyse the fluid flow through the spiral duct geometries with a focus on making detailed comparisons with the flow through axis-symmetric curved ducts. Our analysis ultimately provides an efficient means for estimating spiral duct flow, a robust justification for the use of curved duct flow as an approximation for spiral duct flow in certain regimes and reveals some of the specific differences between the spiral and axis-symmetric curved ducts without being obfuscated by a curvature parameter perturbation. Our methodology is readily applied to study spiral duct of any cross-section shape, including the rectangular cross-sections which are common in a variety of applications.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Applied Mathematical Modelling
数学-工程:综合
CiteScore
9.80
自引率
8.00%
发文量
508
审稿时长
43 days
期刊介绍:
Applied Mathematical Modelling focuses on research related to the mathematical modelling of engineering and environmental processes, manufacturing, and industrial systems. A significant emerging area of research activity involves multiphysics processes, and contributions in this area are particularly encouraged.
This influential publication covers a wide spectrum of subjects including heat transfer, fluid mechanics, CFD, and transport phenomena; solid mechanics and mechanics of metals; electromagnets and MHD; reliability modelling and system optimization; finite volume, finite element, and boundary element procedures; modelling of inventory, industrial, manufacturing and logistics systems for viable decision making; civil engineering systems and structures; mineral and energy resources; relevant software engineering issues associated with CAD and CAE; and materials and metallurgical engineering.
Applied Mathematical Modelling is primarily interested in papers developing increased insights into real-world problems through novel mathematical modelling, novel applications or a combination of these. Papers employing existing numerical techniques must demonstrate sufficient novelty in the solution of practical problems. Papers on fuzzy logic in decision-making or purely financial mathematics are normally not considered. Research on fractional differential equations, bifurcation, and numerical methods needs to include practical examples. Population dynamics must solve realistic scenarios. Papers in the area of logistics and business modelling should demonstrate meaningful managerial insight. Submissions with no real-world application will not be considered.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


