路德维克型弹塑性材料螺旋弹簧的优化结构设计
IF 2.1
Q2 ENGINEERING, MULTIDISCIPLINARY
引用次数: 0
摘要
由于弹簧设计中理想化幂律假设的局限性,这项工作使用更现实的路德维克型弹塑性材料模型重新审视了压缩螺旋弹簧的优化。与以前的方法不同,我们明确地将俯角纳入计算总导线长度,提高几何精度。引入统一的解根算法有效地处理Karush-Kuhn-Tucker条件,消除了逐案处理的需要。提出的设计是针对DIN标准的基准,这在分析研究中经常被忽视。为了确保实际的相关性,在COMSOL中进行了有限元模拟,结果与理论预测吻合良好。精细几何、非线性力学和比较验证的结合提供了一个更强大的优化框架,将理论建模与工程实践联系起来。我们相信这种方法为先进结构材料的弹簧设计提供了新的见解。本文章由计算机程序翻译,如有差异,请以英文原文为准。
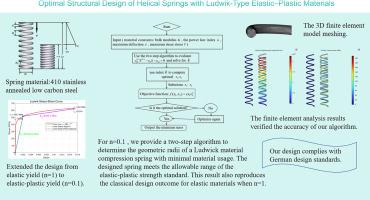
Optimal structural design of helical springs with Ludwik-type elastic–plastic materials
Motivated by the limitations of idealized power-law assumptions in spring design, this work revisits the optimization of compressive helical springs using a more realistic Ludwik-type elastic–perfect plastic material model. Unlike earlier approaches, we explicitly incorporate the pitch angle in computing the total wire length, improving geometric accuracy. A unified root-solving algorithm is introduced to handle the Karush–Kuhn–Tucker conditions efficiently, eliminating the need for case-by-case treatment. The proposed design is benchmarked against the DIN standard, which is often overlooked in analytical studies. To ensure practical relevance, finite element simulations are performed in COMSOL and show good agreement with theoretical predictions. The combination of refined geometry, nonlinear mechanics, and comparative validation provides a more robust optimization framework that bridges theoretical modeling with engineering practice. We believe this approach offers new insight into spring design for advanced structural materials.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Applications in engineering science
Mechanical Engineering
CiteScore
3.60
自引率
0.00%
发文量
0
审稿时长
68 days
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


