缩并自相似群的C*-代数的简单性

IF 2.6 1区物理与天体物理 Q1 PHYSICS, MATHEMATICAL

Communications in Mathematical Physics Pub Date : 2025-09-01 DOI:10.1007/s00220-025-05411-5

Eusebio Gardella, Volodymyr Nekrashevych, Benjamin Steinberg, Alina Vdovina

{"title":"缩并自相似群的C*-代数的简单性","authors":"Eusebio Gardella, Volodymyr Nekrashevych, Benjamin Steinberg, Alina Vdovina","doi":"10.1007/s00220-025-05411-5","DOIUrl":null,"url":null,"abstract":"<div>We show that the \\(C^*\\)-algebra associated by Nekrashevych to a contracting self-similar group is simple if and only if the corresponding complex \\(*\\)-algebra is simple. We also improve on Steinberg and Szakács’s algorithm to determine if the \\(*\\)-algebra is simple. This provides an interesting class of non-Hausdorff, amenable, effective and minimal ample groupoids for which simplicity of the \\(C^*\\)-algebra and the complex \\(*\\)-algebra are equivalent.</div>","PeriodicalId":522,"journal":{"name":"Communications in Mathematical Physics","volume":"406 10","pages":""},"PeriodicalIF":2.6000,"publicationDate":"2025-09-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Simplicity of C*-Algebras of Contracting Self-Similar Groups\",\"authors\":\"Eusebio Gardella, Volodymyr Nekrashevych, Benjamin Steinberg, Alina Vdovina\",\"doi\":\"10.1007/s00220-025-05411-5\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>We show that the \\\\(C^*\\\\)-algebra associated by Nekrashevych to a contracting self-similar group is simple if and only if the corresponding complex \\\\(*\\\\)-algebra is simple. We also improve on Steinberg and Szakács’s algorithm to determine if the \\\\(*\\\\)-algebra is simple. This provides an interesting class of non-Hausdorff, amenable, effective and minimal ample groupoids for which simplicity of the \\\\(C^*\\\\)-algebra and the complex \\\\(*\\\\)-algebra are equivalent.</div>\",\"PeriodicalId\":522,\"journal\":{\"name\":\"Communications in Mathematical Physics\",\"volume\":\"406 10\",\"pages\":\"\"},\"PeriodicalIF\":2.6000,\"publicationDate\":\"2025-09-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Communications in Mathematical Physics\",\"FirstCategoryId\":\"101\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00220-025-05411-5\",\"RegionNum\":1,\"RegionCategory\":\"物理与天体物理\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"PHYSICS, MATHEMATICAL\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Communications in Mathematical Physics","FirstCategoryId":"101","ListUrlMain":"https://link.springer.com/article/10.1007/s00220-025-05411-5","RegionNum":1,"RegionCategory":"物理与天体物理","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"PHYSICS, MATHEMATICAL","Score":null,"Total":0}

引用次数: 0

摘要

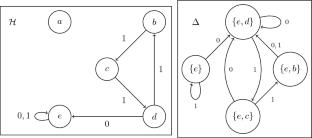
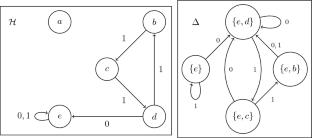
我们证明了Nekrashevych与一个收缩自相似群相关联的\(C^*\) -代数是简单的当且仅当对应的复\(*\) -代数是简单的。我们还改进了Steinberg和Szakács的算法，以确定\(*\) -代数是否简单。这提供了一类有趣的非hausdorff、可服从、有效和最小样本群，其中\(C^*\) -代数和复杂\(*\) -代数的简单性是等价的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

Simplicity of C*-Algebras of Contracting Self-Similar Groups

查看原文本刊更多论文

Simplicity of C*-Algebras of Contracting Self-Similar Groups

We show that the \(C^*\)-algebra associated by Nekrashevych to a contracting self-similar group is simple if and only if the corresponding complex \(*\)-algebra is simple. We also improve on Steinberg and Szakács’s algorithm to determine if the \(*\)-algebra is simple. This provides an interesting class of non-Hausdorff, amenable, effective and minimal ample groupoids for which simplicity of the \(C^*\)-algebra and the complex \(*\)-algebra are equivalent.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Communications in Mathematical Physics 物理-物理：数学物理

CiteScore

4.70

自引率

8.30%

发文量

226

审稿时长

3-6 weeks

期刊介绍： The mission of Communications in Mathematical Physics is to offer a high forum for works which are motivated by the vision and the challenges of modern physics and which at the same time meet the highest mathematical standards.