Šoltés图的基尔霍夫指数问题
IF 3.4
2区 数学
Q1 MATHEMATICS, APPLIED
引用次数: 0
摘要
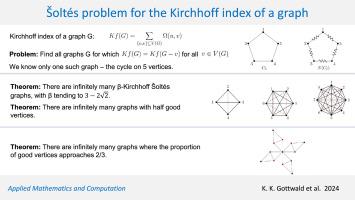
连通图G的Kirchhoff指数Kf(G)定义为G中所有顶点对之间的电阻距离之和。如果去掉v后Kirchhoff指数不变,则称v∈v (G)是一个好顶点,即Kf(G)=Kf(G - v)。1991年,Šoltés研究了图的维纳指数,并提出了识别图的问题,其中任意顶点的移除保留了维纳指数。在本文中,我们探索了一个类似的概念:识别Kirchhoff Šoltés图,即所有顶点都是好顶点的图。我们证明了周期C5是一个Kirchhoff Šoltés图。由于寻找更多这样的图的例子的挑战,我们将注意力转移到Kirchhoff Šoltés问题的几个放松版本,其中主要目标是识别包含至少一个好顶点的图。其中之一是β- kirchhoff Šoltés问题,该问题寻求找到一个无限族图,其中好顶点的比例至少为β,其中β∈(0,1]是指定的有理数。另一个涉及构建无限的图族,其中好顶点的比例随着图阶的增长而增加,并渐近于给定的实数γ∈(0,1)。我们证明了两个松弛版本都有无穷多个解。特别地,我们证明了无限多个图的存在性,其中好顶点的比例β, 1/7≤β<;1/5趋向于某个无理数。进一步,我们证明了具有半好顶点的图的无穷多个存在性,并且对于每一个s∈N,我们构造了一个好顶点的比例趋于s+12s+1的无限族图。这些发现对于解决最初的问题至关重要,即确定是否存在C5之外的其他解决方案。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Šoltés problem for the Kirchhoff index of a graph
The Kirchhoff index of a connected graph is defined as the sum of resistance distances between all pairs of vertices in . We say that is a good vertex if the Kirchhoff index remains unchanged when is removed, i.e. . In 1991, Šoltés studied the Wiener index of a graph and posed the problem of identifying graphs for which the removal of an arbitrary vertex preserves the Wiener index. In this paper, we explore a similar concept: identifying Kirchhoff Šoltés graphs, i.e. graphs in which all vertices are good vertices. We show that the cycle is a Kirchhoff Šoltés graph. Due to the challenge of finding more examples of such graphs, we shift our focus to several relaxed versions of the Kirchhoff Šoltés problem, where the primary objective is to identify graphs containing at least one good vertex. One of them is the -Kirchhoff Šoltés problem, which seeks to find an infinite family of graphs in which the proportion of good vertices is at least , with being a specified rational number. Another one involves constructing infinite families of graphs where the proportion of good vertices increases and asymptotically approaches a given real number as the order of the graph grows. We demonstrate that both relaxed versions have infinitely many solutions. In particular, we prove the existence of infinitely many graphs for which the proportion of good vertices, tends to a certain irrational number. Furthermore, we prove the existence of infinitely many graphs with half good vertices, and for each , we construct an infinite family of graphs whose proportion of good vertices tends to . These findings could be pivotal in addressing the original problem of determining whether there are additional solutions beyond .
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
7.90
自引率
10.00%
发文量
755
审稿时长
36 days
期刊介绍:
Applied Mathematics and Computation addresses work at the interface between applied mathematics, numerical computation, and applications of systems – oriented ideas to the physical, biological, social, and behavioral sciences, and emphasizes papers of a computational nature focusing on new algorithms, their analysis and numerical results.
In addition to presenting research papers, Applied Mathematics and Computation publishes review articles and single–topics issues.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


