粘塑性基体纤维增强复合材料的渐进均质化和损伤建模
IF 3.8
3区 工程技术
Q1 MECHANICS
International Journal of Solids and Structures
Pub Date : 2025-08-22
DOI:10.1016/j.ijsolstr.2025.113614
引用次数: 0
摘要
本工作提出了一种新的方法来执行渐进式计算均匀化和内部损伤建模的纤维增强层结合一个单独的粘塑性基质层。在以基体为主的加载情况下,粘塑性应变在均匀应力场的计算中起着重要的作用,提出的公式尤其有用。首先计算了层和纯基体的层体积分数,并采用Voigt近似,提出了考虑层和基体层降解的宏观尺度(均质)切模量表达式。均匀化切模量的适用性随后通过在内部开发的非线性有限元框架中实现它,同时解决了几个边值问题。结果表明,该方法可以推广到任何具有不同本构响应和非弹性应变的层状介质。本文章由计算机程序翻译,如有差异,请以英文原文为准。
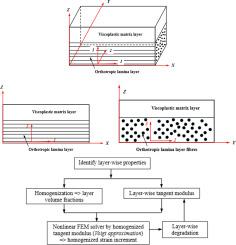
Progressive homogenization and damage modelling of a fibre reinforced composite with a viscoplastic matrix
The present work proposes a novel approach to perform the progressive computational homogenization and internal damage modelling in a fibre reinforced lamina combined with a separate viscoplastic matrix layer. The proposed formulation is especially useful in the matrix-dominated loading cases, where the viscoplastic strain plays an important role in the computation of homogenized stress field. The layer volume fractions of lamina and pure matrix are first computed, and the macro-scale (homogenized) tangent modulus expression is proposed, incorporating the degradation in lamina and matrix layers, employing Voigt approximation. The applicability of the homogenized tangent modulus is subsequently demonstrated by implementing it in an in-house developed non-linear finite element framework while solving several boundary value problems. It is also demonstrated that, the presented approach can be extended to any layered media having different constitutive responses and inelastic strain.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
6.70
自引率
8.30%
发文量
405
审稿时长
70 days
期刊介绍:
The International Journal of Solids and Structures has as its objective the publication and dissemination of original research in Mechanics of Solids and Structures as a field of Applied Science and Engineering. It fosters thus the exchange of ideas among workers in different parts of the world and also among workers who emphasize different aspects of the foundations and applications of the field.
Standing as it does at the cross-roads of Materials Science, Life Sciences, Mathematics, Physics and Engineering Design, the Mechanics of Solids and Structures is experiencing considerable growth as a result of recent technological advances. The Journal, by providing an international medium of communication, is encouraging this growth and is encompassing all aspects of the field from the more classical problems of structural analysis to mechanics of solids continually interacting with other media and including fracture, flow, wave propagation, heat transfer, thermal effects in solids, optimum design methods, model analysis, structural topology and numerical techniques. Interest extends to both inorganic and organic solids and structures.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


