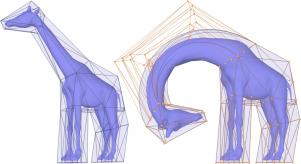
Polynomial 3D Green coordinates and their derivatives for linear cages

We derive closed-form expressions for polynomial Green coordinates and their derivatives for 3D linear cages. The keys to our derivation are the integrals of polynomials divided by Euclidean distance over a triangle and their derivatives. We demonstrate the usefulness of our polynomial 3D Green coordinates and derivatives on cage-based and variational shape deformations. In cage-based deformation, the coordinates enable deformation from linear polygons of the input cage to polynomial surfaces of any order, allowing users to perform intuitive deformations with a small number of input parameters. In variational deformation, the coordinates and derivatives form a smooth deformation subspace, allowing for the realization of nonlinear shape optimization.