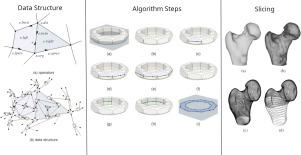
TSlicer: An optimal topology-based slicing algorithm for Z-monotone 3D meshes

We address a computational problem that is an essential step in computer graphics, 3D printing, and many other processes: namely, the slicing of a 3D polygonal structured mesh model (as can be extracted from an STL, OBJ, or 3MF file) by a set of parallel planes. We describe TSlicer, a sweep-plane algorithm that exploits the topological information provided by the mesh data structure to reduce the number of intersection tests. The output is a set of polygons on each cutting plane. The topological information allows us to produce the sides of these polygons directly in the proper sequence and orientation. Furthermore, a key optimization is proposed to a topological data structure to speed up the traversal of meshes with any Z-monotone polygons as faces. We show that TSlicer is optimal in the asymptotic worst-case sense, and, according to experiments, substantially faster than a previous method for slicing unstructured triangle list models, as provided by STL files. The source code and mesh models used in this study are available on GitHub.¹