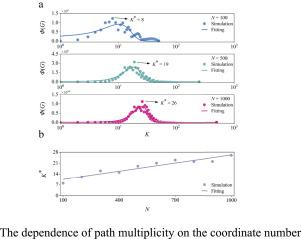
Path multiplicity in regular ring lattices

Regular ring lattices have attracted significant attention in the complex network field due to their structured connectivity and their role as foundational models for studying network properties like clustering, robustness, and the transition to small-world characteristics. However, path multiplicity, defined as the number of shortest paths connecting pairs of nodes, has been largely overlooked in such networks. Here, we thoroughly discuss the path multiplicity between any node pair, as well as the average across all pairs, within regular ring lattices using analytical and simulation methods. We analytically derive the number of shortest paths between two nodes and analyze the corresponding distribution numerically. Our findings reveal notable variations in the shape and range of the distribution with varying coordinate number $K$. We also examine the dependence of the average path multiplicity on $K$ and network size $N$. Our results suggest that, for fixed $N$, the average path multiplicity follows a unimodal pattern with intrinsic fluctuations as $K$ increases, which is well captured by a Gaussian fit. Furthermore, for fixed $K$, the average path multiplicity increases exponentially with $N$. This study enhances the understanding of path multiplicity in regular ring lattices and has potential applications in the design of fault-tolerant communication networks and distributed algorithms.