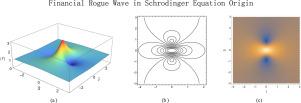
Going beyond the Black–Scholes option pricing model: Financial rogue waves in quantum mechanics

This paper proposes a nonlinear alternative for the Black–Scholes option pricing model defined as the Schrödinger equation. The Black–Scholes equation is obtained from the Schrödinger equation in the leading-order approximation of an asymptotic perturbation theory under the assumptions of weak nonlinearity and weak dispersion. It models the controlled Brownian motion of the financial market and describes the option price wave function in quantum mechanic origin. Here, we analytically predict the existence of a family of financial rogue wave solutions of the Black–Scholes equation in the form of complex rational functions by using symbolic computation. The obtained solutions are composed of a single symmetric soliton or several solitary peaks. The existence of non-zero offset parameters provides nontrivial alterations to higher order solutions as they would decompose into first order ones that can be used to simulate the evolution of financial risks. The financial rogue wave solution demonstrates a condition that investors may face considerable risk or return in the financial market, which might be an actual theoretical basis for its existence. Our study is the first to prove the connection between option pricing and quantum mechanics, which opens a novel path for the excitation and control of financial waveforms of quantum mechanic footprint and extreme financial crisis. Currently, there are no similar studies, making this work crucial and significant for the advancement of quantum finance.