Étale几何起源的动机
IF 0.9
3区 数学
Q2 MATHEMATICS
引用次数: 0
摘要
在qcqs有限维格式上,我们证明了几何起源的可变动机可以用纯范畴的可构造性来表征,从而给出了“所有可构造的可变动机都来自几何吗?”这可以追溯到Cisinski和dsamglise的研究。我们还证明了它们具有连续性,并且满足h下降和Milnor切除。本文章由计算机程序翻译,如有差异,请以英文原文为准。
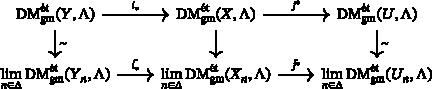



Étale motives of geometric origin
Over qcqs finite-dimensional schemes, we prove that étale motives of geometric origin can be characterised by a constructibility property which is purely categorical, giving a full answer to the question ‘Do all constructible étale motives come from geometry?’ which dates back to Cisinski and Déglise's work. We also show that they afford the continuity property and satisfy h-descent and Milnor excision.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
198
审稿时长
4-8 weeks
期刊介绍:
Published by Oxford University Press prior to January 2017: http://blms.oxfordjournals.org/

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


