非紧致曲面、三角形和刚性
IF 0.9
3区 数学
Q2 MATHEMATICS
引用次数: 0
摘要
证明了每个非紧曲面都具有(3,6)紧三角化,并给出了r3 ${\mathbb {R}}^3$中可数杆节点框架的一般刚度的应用。特别地,每个非紧曲面都具有最小3刚性的(3,6)紧三角剖分。对Richards关于Kerékjártó非紧曲面分类的证明进行了简化。本文章由计算机程序翻译,如有差异,请以英文原文为准。
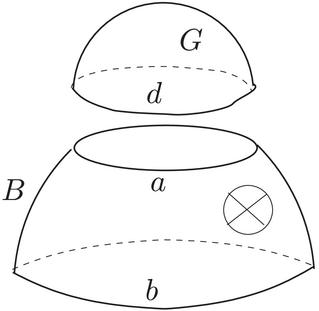



Noncompact surfaces, triangulations and rigidity
Every noncompact surface is shown to have a (3,6)-tight triangulation, and applications are given to the generic rigidity of countable bar-joint frameworks in . In particular, every noncompact surface has a (3,6)-tight triangulation that is minimally 3-rigid. A simplification of Richards' proof of Kerékjártó's classification of noncompact surfaces is also given.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
198
审稿时长
4-8 weeks
期刊介绍:
Published by Oxford University Press prior to January 2017: http://blms.oxfordjournals.org/

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


