局部和非局部系统的De Giorgi方法

IF 1.2 2区数学 Q1 MATHEMATICS

Journal of the London Mathematical Society-Second Series Pub Date : 2025-07-22 DOI:10.1112/jlms.70237

Linus Behn, Lars Diening, Simon Nowak, Toni Scharle

{"title":"局部和非局部系统的De Giorgi方法","authors":"Linus Behn, Lars Diening, Simon Nowak, Toni Scharle","doi":"10.1112/jlms.70237","DOIUrl":null,"url":null,"abstract":"<p>We extend the De Giorgi iteration technique to the vectorial setting. For this we replace the usual scalar truncation operator by a vectorial shortening operator. As an application, we prove local boundedness for local and nonlocal nonlinear systems. Furthermore, we show convex hull properties, which are a generalization of the maximum principle to the case of systems.</p>","PeriodicalId":49989,"journal":{"name":"Journal of the London Mathematical Society-Second Series","volume":"112 1","pages":""},"PeriodicalIF":1.2000,"publicationDate":"2025-07-22","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.70237","citationCount":"0","resultStr":"{\"title\":\"The De Giorgi method for local and nonlocal systems\",\"authors\":\"Linus Behn, Lars Diening, Simon Nowak, Toni Scharle\",\"doi\":\"10.1112/jlms.70237\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>We extend the De Giorgi iteration technique to the vectorial setting. For this we replace the usual scalar truncation operator by a vectorial shortening operator. As an application, we prove local boundedness for local and nonlocal nonlinear systems. Furthermore, we show convex hull properties, which are a generalization of the maximum principle to the case of systems.</p>\",\"PeriodicalId\":49989,\"journal\":{\"name\":\"Journal of the London Mathematical Society-Second Series\",\"volume\":\"112 1\",\"pages\":\"\"},\"PeriodicalIF\":1.2000,\"publicationDate\":\"2025-07-22\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.70237\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of the London Mathematical Society-Second Series\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://londmathsoc.onlinelibrary.wiley.com/doi/10.1112/jlms.70237\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of the London Mathematical Society-Second Series","FirstCategoryId":"100","ListUrlMain":"https://londmathsoc.onlinelibrary.wiley.com/doi/10.1112/jlms.70237","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

我们将De Giorgi迭代技术扩展到向量设置。为此，我们将通常的标量截断算子替换为矢量缩短算子。作为应用，我们证明了局部和非局部非线性系统的局部有界性。进一步，我们证明了凸包性质，这是极大值原理在系统情况下的推广。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

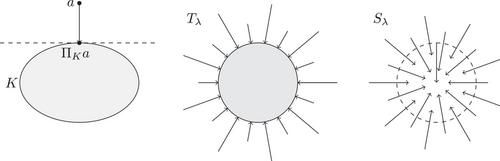
The De Giorgi method for local and nonlocal systems

查看原文本刊更多论文

The De Giorgi method for local and nonlocal systems

We extend the De Giorgi iteration technique to the vectorial setting. For this we replace the usual scalar truncation operator by a vectorial shortening operator. As an application, we prove local boundedness for local and nonlocal nonlinear systems. Furthermore, we show convex hull properties, which are a generalization of the maximum principle to the case of systems.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of the London Mathematical Society-Second Series 数学-数学

CiteScore

1.90

自引率

0.00%

发文量

186

审稿时长

6-12 weeks

期刊介绍： The Journal of the London Mathematical Society has been publishing leading research in a broad range of mathematical subject areas since 1926. The Journal welcomes papers on subjects of general interest that represent a significant advance in mathematical knowledge, as well as submissions that are deemed to stimulate new interest and research activity.