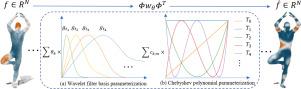
L2-GNN: Graph neural networks with fast spectral filters using twice linear parameterization

To improve learning on irregular 3D shapes, such as meshes with varying discretizations and point clouds with different samplings, we propose L${}^2$-GNN, a new graph neural network that approximates the spectral filters using twice linear parameterization. First, we parameterize the spectral filters using wavelet filter basis functions. The parameterization allows for an enlarged receptive field of graph convolutions, which can simultaneously capture low-frequency and high-frequency information. Second, we parameterize the wavelet filter basis functions using Chebyshev polynomial basis functions. This parameterization reduces the computational complexity of graph convolutions while maintaining robustness to the change of mesh discretization and point cloud sampling. Our L${}^2$-GNN based on the fast spectral filter can be used for shape correspondence, classification, and segmentation tasks on non-regular mesh or point cloud data. Experimental results show that our method outperforms the current state of the art in terms of both quality and efficiency.