Clifford表示通过一致代数秩
IF 1.2
2区 数学
Q1 MATHEMATICS
Journal of the London Mathematical Society-Second Series
Pub Date : 2025-06-02
DOI:10.1112/jlms.70193
引用次数: 0
摘要
本文引入了有限图上一个除数类的一致代数秩。我们证明了它位于Caporaso的代数秩和Baker和Norine的组合秩之间。证明了一致代数秩的Riemann-Roch定理,并证明了代数秩和一致代数秩在有效因子上都是可以实现的。作为应用,我们利用一致代数秩来证明Clifford表示总是存在的。最后,我们明确地描述了一类图的Clifford表示。本文章由计算机程序翻译,如有差异,请以英文原文为准。
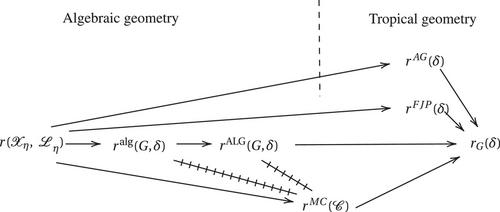
Clifford representatives via the uniform algebraic rank
In this paper, we introduce the uniform algebraic rank of a divisor class on a finite graph. We show that it lies between Caporaso's algebraic rank and the combinatorial rank of Baker and Norine. We prove the Riemann–Roch theorem for the uniform algebraic rank, and show that both the algebraic and the uniform algebraic rank are realized on effective divisors. As an application, we use the uniform algebraic rank to show that Clifford representatives always exist. We conclude with an explicit description of such Clifford representatives for a large class of graphs.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
186
审稿时长
6-12 weeks
期刊介绍:
The Journal of the London Mathematical Society has been publishing leading research in a broad range of mathematical subject areas since 1926. The Journal welcomes papers on subjects of general interest that represent a significant advance in mathematical knowledge, as well as submissions that are deemed to stimulate new interest and research activity.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


