单层修饰过渡金属氮化物中的真陈氏绝缘子
IF 19
1区 材料科学
Q1 CHEMISTRY, MULTIDISCIPLINARY
Yilin Han, Tingli He, Run-Wu Zhang, ZhenHua Li, Zhi-Ming Yu, Yugui Yao
{"title":"单层修饰过渡金属氮化物中的真陈氏绝缘子","authors":"Yilin Han, Tingli He, Run-Wu Zhang, ZhenHua Li, Zhi-Ming Yu, Yugui Yao","doi":"10.1002/adfm.202505282","DOIUrl":null,"url":null,"abstract":"A trend in recent research is to push the study of topological phases to the spin-splitting antiferromagnetic (SSAFM) systems, which has become a research forefront of spintronics. Here, the realization of SSAFM real Chern insulator (RCI) in the monolayer transition metal nitride A(BN)<sub>2</sub> (A = Mg, Ca, Zn and B = Co) is revealed. Taking monolayer Mg(CoN)<sub>2</sub> (ML-MgCoN) as an example. In the absence of spin-orbit coupling, the ML-MgCoN is an altermagnetic (AM) material, and each spin channel of the material possesses a nontrivial real Chern number protected by <span data-altimg=\"/cms/asset/4a927a4a-16d8-47ea-b068-f751a98e1ed9/adfm202505282-math-0001.png\"></span><mjx-container ctxtmenu_counter=\"2\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adfm202505282-math-0001.png\"><mjx-semantics><mjx-mrow data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"5,6\" data-semantic-content=\"7\" data-semantic- data-semantic-role=\"implicit\" data-semantic-speech=\"upper C Subscript 2 z Baseline script upper T\" data-semantic-type=\"infixop\"><mjx-msub data-semantic-children=\"0,4\" data-semantic- data-semantic-parent=\"8\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em; margin-left: -0.045em;\"><mjx-mrow data-semantic-annotation=\"clearspeak:simple;clearspeak:unit\" data-semantic-children=\"1,2\" data-semantic-content=\"3\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\" size=\"s\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"4\" data-semantic-role=\"integer\" data-semantic-type=\"number\"><mjx-c></mjx-c></mjx-mn><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,\" data-semantic-parent=\"4\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"4\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-script></mjx-msub><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,\" data-semantic-parent=\"8\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\" style=\"margin-left: 0.056em; margin-right: 0.056em;\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"script\" data-semantic- data-semantic-parent=\"8\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:1616301X:media:adfm202505282:adfm202505282-math-0001\" display=\"inline\" location=\"graphic/adfm202505282-math-0001.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"5,6\" data-semantic-content=\"7\" data-semantic-role=\"implicit\" data-semantic-speech=\"upper C Subscript 2 z Baseline script upper T\" data-semantic-type=\"infixop\"><msub data-semantic-=\"\" data-semantic-children=\"0,4\" data-semantic-parent=\"8\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">C</mi><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple;clearspeak:unit\" data-semantic-children=\"1,2\" data-semantic-content=\"3\" data-semantic-parent=\"5\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\"><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"4\" data-semantic-role=\"integer\" data-semantic-type=\"number\">2</mn><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,\" data-semantic-parent=\"4\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"></mo><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"4\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">z</mi></mrow></msub><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,\" data-semantic-parent=\"8\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"></mo><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"script\" data-semantic-parent=\"8\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"script\">T</mi></mrow>$C_{2z}{\\cal T}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> symmetry. Unlike conventional RCIs, the multi-atomic-layer structure and altermagnetism of ML-MgCoN lead to the emergence of two sets of corner states exhibiting opposite layer and spin polarizations. Under out-of-plane electric field (<i>E</i><sub><i>z</i></sub>) and uniaxial strain, the ML-MgCoN is no longer an AM material but still a SSAFM material with <span data-altimg=\"/cms/asset/840a441c-739e-489f-954c-3a651bde651a/adfm202505282-math-0002.png\"></span><mjx-container ctxtmenu_counter=\"3\" ctxtmenu_oldtabindex=\"1\" jax=\"CHTML\" role=\"application\" sre-explorer- style=\"font-size: 103%; position: relative;\" tabindex=\"0\"><mjx-math aria-hidden=\"true\" location=\"graphic/adfm202505282-math-0002.png\"><mjx-semantics><mjx-mrow data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"5,6\" data-semantic-content=\"7\" data-semantic- data-semantic-role=\"implicit\" data-semantic-speech=\"upper C Subscript 2 z Baseline script upper T\" data-semantic-type=\"infixop\"><mjx-msub data-semantic-children=\"0,4\" data-semantic- data-semantic-parent=\"8\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\"vertical-align: -0.15em; margin-left: -0.045em;\"><mjx-mrow data-semantic-annotation=\"clearspeak:simple;clearspeak:unit\" data-semantic-children=\"1,2\" data-semantic-content=\"3\" data-semantic- data-semantic-parent=\"5\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\" size=\"s\"><mjx-mn data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic- data-semantic-parent=\"4\" data-semantic-role=\"integer\" data-semantic-type=\"number\"><mjx-c></mjx-c></mjx-mn><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,\" data-semantic-parent=\"4\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic- data-semantic-parent=\"4\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-script></mjx-msub><mjx-mo data-semantic-added=\"true\" data-semantic- data-semantic-operator=\"infixop,\" data-semantic-parent=\"8\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\" style=\"margin-left: 0.056em; margin-right: 0.056em;\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"script\" data-semantic- data-semantic-parent=\"8\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\"inline\" unselectable=\"on\"><math altimg=\"urn:x-wiley:1616301X:media:adfm202505282:adfm202505282-math-0002\" display=\"inline\" location=\"graphic/adfm202505282-math-0002.png\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><semantics><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:unit\" data-semantic-children=\"5,6\" data-semantic-content=\"7\" data-semantic-role=\"implicit\" data-semantic-speech=\"upper C Subscript 2 z Baseline script upper T\" data-semantic-type=\"infixop\"><msub data-semantic-=\"\" data-semantic-children=\"0,4\" data-semantic-parent=\"8\" data-semantic-role=\"latinletter\" data-semantic-type=\"subscript\"><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"5\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">C</mi><mrow data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple;clearspeak:unit\" data-semantic-children=\"1,2\" data-semantic-content=\"3\" data-semantic-parent=\"5\" data-semantic-role=\"implicit\" data-semantic-type=\"infixop\"><mn data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"normal\" data-semantic-parent=\"4\" data-semantic-role=\"integer\" data-semantic-type=\"number\">2</mn><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,\" data-semantic-parent=\"4\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"></mo><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"italic\" data-semantic-parent=\"4\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\">z</mi></mrow></msub><mo data-semantic-=\"\" data-semantic-added=\"true\" data-semantic-operator=\"infixop,\" data-semantic-parent=\"8\" data-semantic-role=\"multiplication\" data-semantic-type=\"operator\"></mo><mi data-semantic-=\"\" data-semantic-annotation=\"clearspeak:simple\" data-semantic-font=\"script\" data-semantic-parent=\"8\" data-semantic-role=\"latinletter\" data-semantic-type=\"identifier\" mathvariant=\"script\">T</mi></mrow>$C_{2z}{\\cal T}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> symmetry in each spin channel. Moreover, the degeneracy of the two sets of topological corner states is lifted, suggesting a selective control of layer and spin polarizations under external fields. This work not only significantly broadens the material database of AM RCI, but also reveals a new mechanism to control the spin in spintronics.","PeriodicalId":112,"journal":{"name":"Advanced Functional Materials","volume":"29 1","pages":""},"PeriodicalIF":19.0000,"publicationDate":"2025-05-16","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Real Chern Insulator in Monolayer Decorated Transition Metal Nitrides\",\"authors\":\"Yilin Han, Tingli He, Run-Wu Zhang, ZhenHua Li, Zhi-Ming Yu, Yugui Yao\",\"doi\":\"10.1002/adfm.202505282\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"A trend in recent research is to push the study of topological phases to the spin-splitting antiferromagnetic (SSAFM) systems, which has become a research forefront of spintronics. Here, the realization of SSAFM real Chern insulator (RCI) in the monolayer transition metal nitride A(BN)<sub>2</sub> (A = Mg, Ca, Zn and B = Co) is revealed. Taking monolayer Mg(CoN)<sub>2</sub> (ML-MgCoN) as an example. In the absence of spin-orbit coupling, the ML-MgCoN is an altermagnetic (AM) material, and each spin channel of the material possesses a nontrivial real Chern number protected by <span data-altimg=\\\"/cms/asset/4a927a4a-16d8-47ea-b068-f751a98e1ed9/adfm202505282-math-0001.png\\\"></span><mjx-container ctxtmenu_counter=\\\"2\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adfm202505282-math-0001.png\\\"><mjx-semantics><mjx-mrow data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"5,6\\\" data-semantic-content=\\\"7\\\" data-semantic- data-semantic-role=\\\"implicit\\\" data-semantic-speech=\\\"upper C Subscript 2 z Baseline script upper T\\\" data-semantic-type=\\\"infixop\\\"><mjx-msub data-semantic-children=\\\"0,4\\\" data-semantic- data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em; margin-left: -0.045em;\\\"><mjx-mrow data-semantic-annotation=\\\"clearspeak:simple;clearspeak:unit\\\" data-semantic-children=\\\"1,2\\\" data-semantic-content=\\\"3\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\" size=\\\"s\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\"><mjx-c></mjx-c></mjx-mn><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-script></mjx-msub><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\" style=\\\"margin-left: 0.056em; margin-right: 0.056em;\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"script\\\" data-semantic- data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:1616301X:media:adfm202505282:adfm202505282-math-0001\\\" display=\\\"inline\\\" location=\\\"graphic/adfm202505282-math-0001.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"5,6\\\" data-semantic-content=\\\"7\\\" data-semantic-role=\\\"implicit\\\" data-semantic-speech=\\\"upper C Subscript 2 z Baseline script upper T\\\" data-semantic-type=\\\"infixop\\\"><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"0,4\\\" data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">C</mi><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple;clearspeak:unit\\\" data-semantic-children=\\\"1,2\\\" data-semantic-content=\\\"3\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\"><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">2</mn><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"></mo><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">z</mi></mrow></msub><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"></mo><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"script\\\" data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"script\\\">T</mi></mrow>$C_{2z}{\\\\cal T}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> symmetry. Unlike conventional RCIs, the multi-atomic-layer structure and altermagnetism of ML-MgCoN lead to the emergence of two sets of corner states exhibiting opposite layer and spin polarizations. Under out-of-plane electric field (<i>E</i><sub><i>z</i></sub>) and uniaxial strain, the ML-MgCoN is no longer an AM material but still a SSAFM material with <span data-altimg=\\\"/cms/asset/840a441c-739e-489f-954c-3a651bde651a/adfm202505282-math-0002.png\\\"></span><mjx-container ctxtmenu_counter=\\\"3\\\" ctxtmenu_oldtabindex=\\\"1\\\" jax=\\\"CHTML\\\" role=\\\"application\\\" sre-explorer- style=\\\"font-size: 103%; position: relative;\\\" tabindex=\\\"0\\\"><mjx-math aria-hidden=\\\"true\\\" location=\\\"graphic/adfm202505282-math-0002.png\\\"><mjx-semantics><mjx-mrow data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"5,6\\\" data-semantic-content=\\\"7\\\" data-semantic- data-semantic-role=\\\"implicit\\\" data-semantic-speech=\\\"upper C Subscript 2 z Baseline script upper T\\\" data-semantic-type=\\\"infixop\\\"><mjx-msub data-semantic-children=\\\"0,4\\\" data-semantic- data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi><mjx-script style=\\\"vertical-align: -0.15em; margin-left: -0.045em;\\\"><mjx-mrow data-semantic-annotation=\\\"clearspeak:simple;clearspeak:unit\\\" data-semantic-children=\\\"1,2\\\" data-semantic-content=\\\"3\\\" data-semantic- data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\" size=\\\"s\\\"><mjx-mn data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic- data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\"><mjx-c></mjx-c></mjx-mn><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic- data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-script></mjx-msub><mjx-mo data-semantic-added=\\\"true\\\" data-semantic- data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\" style=\\\"margin-left: 0.056em; margin-right: 0.056em;\\\"><mjx-c></mjx-c></mjx-mo><mjx-mi data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"script\\\" data-semantic- data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\"><mjx-c></mjx-c></mjx-mi></mjx-mrow></mjx-semantics></mjx-math><mjx-assistive-mml display=\\\"inline\\\" unselectable=\\\"on\\\"><math altimg=\\\"urn:x-wiley:1616301X:media:adfm202505282:adfm202505282-math-0002\\\" display=\\\"inline\\\" location=\\\"graphic/adfm202505282-math-0002.png\\\" xmlns=\\\"http://www.w3.org/1998/Math/MathML\\\"><semantics><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:unit\\\" data-semantic-children=\\\"5,6\\\" data-semantic-content=\\\"7\\\" data-semantic-role=\\\"implicit\\\" data-semantic-speech=\\\"upper C Subscript 2 z Baseline script upper T\\\" data-semantic-type=\\\"infixop\\\"><msub data-semantic-=\\\"\\\" data-semantic-children=\\\"0,4\\\" data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"subscript\\\"><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">C</mi><mrow data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple;clearspeak:unit\\\" data-semantic-children=\\\"1,2\\\" data-semantic-content=\\\"3\\\" data-semantic-parent=\\\"5\\\" data-semantic-role=\\\"implicit\\\" data-semantic-type=\\\"infixop\\\"><mn data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"normal\\\" data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"integer\\\" data-semantic-type=\\\"number\\\">2</mn><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"></mo><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"italic\\\" data-semantic-parent=\\\"4\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\">z</mi></mrow></msub><mo data-semantic-=\\\"\\\" data-semantic-added=\\\"true\\\" data-semantic-operator=\\\"infixop,\\\" data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"multiplication\\\" data-semantic-type=\\\"operator\\\"></mo><mi data-semantic-=\\\"\\\" data-semantic-annotation=\\\"clearspeak:simple\\\" data-semantic-font=\\\"script\\\" data-semantic-parent=\\\"8\\\" data-semantic-role=\\\"latinletter\\\" data-semantic-type=\\\"identifier\\\" mathvariant=\\\"script\\\">T</mi></mrow>$C_{2z}{\\\\cal T}$</annotation></semantics></math></mjx-assistive-mml></mjx-container> symmetry in each spin channel. Moreover, the degeneracy of the two sets of topological corner states is lifted, suggesting a selective control of layer and spin polarizations under external fields. This work not only significantly broadens the material database of AM RCI, but also reveals a new mechanism to control the spin in spintronics.\",\"PeriodicalId\":112,\"journal\":{\"name\":\"Advanced Functional Materials\",\"volume\":\"29 1\",\"pages\":\"\"},\"PeriodicalIF\":19.0000,\"publicationDate\":\"2025-05-16\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Advanced Functional Materials\",\"FirstCategoryId\":\"88\",\"ListUrlMain\":\"https://doi.org/10.1002/adfm.202505282\",\"RegionNum\":1,\"RegionCategory\":\"材料科学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"CHEMISTRY, MULTIDISCIPLINARY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Advanced Functional Materials","FirstCategoryId":"88","ListUrlMain":"https://doi.org/10.1002/adfm.202505282","RegionNum":1,"RegionCategory":"材料科学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}
引用次数: 0
摘要
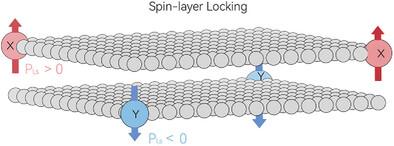
将拓扑相的研究推向自旋分裂反铁磁系统(SSAFM)已成为近年来自旋电子学的研究前沿。本文介绍了在单层过渡金属氮化物A(BN)2 (A = Mg, Ca, Zn, B = Co)中实现SSAFM实陈氏绝缘子(RCI)的方法。以单层Mg(CoN)2 (ML-MgCoN)为例。在没有自旋-轨道耦合的情况下,ML-MgCoN是一种互磁(AM)材料,材料的每个自旋通道都具有一个非平凡的实陈恩数,受C2 _ z _ T$C_{2z}{\cal T}$对称性保护。与传统rci不同,ML-MgCoN的多原子层结构和交变磁性导致出现两组具有相反层和自旋极化的角态。在面外电场(Ez)和单轴应变作用下,ML-MgCoN不再是AM材料,而仍然是SSAFM材料,每个自旋通道具有C2 _ z _ T$C_{2z}{\cal T}$对称性。此外,还提高了两组拓扑角态的简并性,表明在外场作用下,层极化和自旋极化存在选择性控制。这项工作不仅大大拓宽了AM RCI的材料数据库,而且揭示了自旋电子学中控制自旋的新机制。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Real Chern Insulator in Monolayer Decorated Transition Metal Nitrides
A trend in recent research is to push the study of topological phases to the spin-splitting antiferromagnetic (SSAFM) systems, which has become a research forefront of spintronics. Here, the realization of SSAFM real Chern insulator (RCI) in the monolayer transition metal nitride A(BN)2 (A = Mg, Ca, Zn and B = Co) is revealed. Taking monolayer Mg(CoN)2 (ML-MgCoN) as an example. In the absence of spin-orbit coupling, the ML-MgCoN is an altermagnetic (AM) material, and each spin channel of the material possesses a nontrivial real Chern number protected by
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Advanced Functional Materials
工程技术-材料科学:综合
CiteScore
29.50
自引率
4.20%
发文量
2086
审稿时长
2.1 months
期刊介绍:
Firmly established as a top-tier materials science journal, Advanced Functional Materials reports breakthrough research in all aspects of materials science, including nanotechnology, chemistry, physics, and biology every week.
Advanced Functional Materials is known for its rapid and fair peer review, quality content, and high impact, making it the first choice of the international materials science community.
×
引用
GB/T 7714-2015
复制
MLA
复制
APA
复制
导出至
BibTeX
EndNote
RefMan
NoteFirst
NoteExpress
请完成安全验证×
微信好友
朋友圈
QQ好友
复制链接
取消

已复制链接
快去分享给好友吧!
我知道了

点击右上角分享
相关文献
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:
