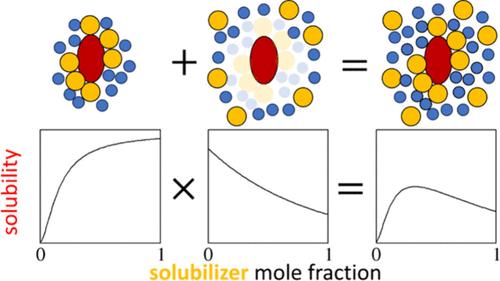
Multiplicativity in Solubility Isotherms

With the help of isotherm equations, how solubility changes with solubilizer concentration (“solubility isotherm”) can reveal the underlying interactions. However, despite their success in elucidating the mechanisms of hydrotropy (via the cooperative (sigmoidal) isotherm) and synergistic solvation (via the quadratic (bell-shaped) isotherm), these simple statistical thermodynamic isotherm equations alone are insufficient for more complex isotherms that combine their features. Here, we show (i) how simple isotherms can be combined via the isotherm multiplicativity rule founded on the excess number relationship (i.e., solubilizer concentration dependence of the solubilizer excess number around a solute) and (ii) how (i) leads to successful modeling of complex solubility isotherms, capturing that cooperative solute–solubilizer association, in turn, induces the exclusion of solubilizers from the already crowded solute’s locality at higher concentrations. Moreover, we will demonstrate that both the cooperative and quadratic solubility isotherms can be derived directly from the excess number relationship, establishing it not only as the basis for the multiplicativity rule but also as the fundamental relationship for simple and complex solubility isotherms.