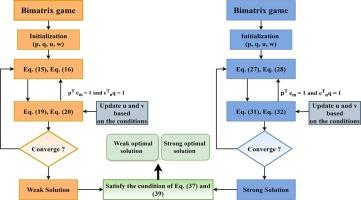
Existence of optimal strategies in bimatrix game and applications

This paper delves into interval-valued bimatrix games, where precise payoffs remain elusive, but lower and upper bounds on payoffs can be determined. The study explores several key questions in this context. Firstly, it addresses the issue of the existence of a universally applicable equilibrium across all instances of interval values. The paper establishes a fundamental equivalence by demonstrating that this property hinges on the solvability of a specific system of interval linear inequalities. Secondly, the research endeavors to characterize the comprehensive set of weak and strong equilibrium using a system of interval linear inequalities. The findings in this paper shed light on the complexities and intricacies of interval-valued bimatrix games, offering valuable insights into their equilibrium properties and computational aspects. Through illustrative examples, we underscore the practical utility of these approaches and compare them with previously developed state-of-the-art methods, demonstrating their ability to generate conservative solutions in the face of interval uncertainty. The findings of this research not only offer valuable insights into the equilibrium properties and computational aspects of interval-valued bimatrix games but extend their practical implications. In particular, the paper delves into real-life applications, exemplifying the significance of these findings for crude oil trading decision-making.