环形-分裂环形-立方体过渡光子学中的拓扑和曲率效应
IF 21.1
1区 材料科学
Q1 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
摘要
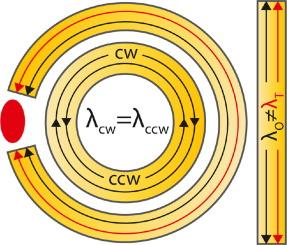
人们正在积极研究各种材料中的拓扑转变,包括拓扑量子相变,超越了朗道理论和有序参数的概念。在此,我们以平面介质环和分裂环之间的过渡及其进一步弯曲成矩形法布里-佩罗共振器为例,提出了两种不同拓扑结构之间的过渡概念。通过实验和理论,我们发现环的 CW-CCW 光子模式的退行性被解除,并形成了两个系列:拓扑模式和普通模式,前者获得了额外的相位 π,相当于薄莫比乌斯带中的贝里相位,后者则没有获得额外的相位。拓扑模式产生的原因是,当间隙的角度从零增加到一度时,场的一个反节点会被间隙逐渐 "切割 "成两个反节点。因此,利用具有可变曲率和固定长度的拓扑法布里-佩罗共振器,可以实现具有任意非整数波的共振模式,并创造出新一代共振器,具有独特的经典和量子应用前景。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Topology and curvature effects in the photonics of ring – split ring – cuboid transitions
Topological transitions in various materials are actively being studied, including topological quantum phase transitions, going beyond the Landau theory and the concept of the order parameter. Here we propose the concept of a transition between two structures with different topology using the example of the transition between a flat dielectric ring and a split ring and its further unbending into a rectangular Fabry-Pérot resonator. Experimentally and theoretically, we discovered the lifting of the degeneracy of the CW-CCW photonic modes of the ring and the formation of two families: topological, which acquire an additional phase , equal to the Berry phase in a thin Möbius strip, and ordinary ones, which do not acquire an additional phase. Topological modes arise due to the gradual “cutting” of one antinode of the field by a gap into two antinodes as the angular size of the gap increases from zero to one degree. Thus, using a topological Fabry-Pérot resonator with variable curvature and fixed length, resonant modes with an arbitrary non-integer number of waves are realized and a new generation of resonators is created with the prospect of unique classical and quantum applications.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Materials Today
工程技术-材料科学:综合
CiteScore
36.30
自引率
1.20%
发文量
237
审稿时长
23 days
期刊介绍:
Materials Today is the leading journal in the Materials Today family, focusing on the latest and most impactful work in the materials science community. With a reputation for excellence in news and reviews, the journal has now expanded its coverage to include original research and aims to be at the forefront of the field.
We welcome comprehensive articles, short communications, and review articles from established leaders in the rapidly evolving fields of materials science and related disciplines. We strive to provide authors with rigorous peer review, fast publication, and maximum exposure for their work. While we only accept the most significant manuscripts, our speedy evaluation process ensures that there are no unnecessary publication delays.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


