采样数据 Lipschitz 非线性系统的鲁棒模型预测控制:灵活关节机器人的应用
IF 2.6
3区 计算机科学
Q2 AUTOMATION & CONTROL SYSTEMS
引用次数: 0
摘要
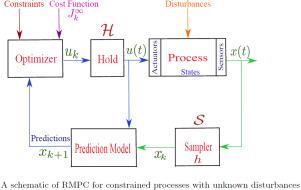
在过去二十年里,柔性关节机器人的控制引起了许多业内专业人士的关注。这是一项艰巨的任务,因为当我们在这些机器人的控制设计中考虑到关节柔性时,就会失去使刚性机器人的控制更容易的各种结构特征,例如电机转矩对链接速度的被动性、完全致动以及对每个关节的单独控制。然而,我们在设计控制器时必须考虑关节的灵活性,否则系统可能会变得不稳定。在本文中,我们为柔性关节机器人设计了一种鲁棒模型预测控制器方案,该机器人被建模为具有未知有界干扰的采样数据 Lipschitz 非线性系统。假设系统的状态可用于反馈。因此,利用鲁棒稳定性准则设计了一个状态反馈控制法则,并可通过求解在线优化问题来计算。该控制法则通过降低最坏情况值来优化性能指标。所提出的控制设计方案被应用于单链柔性关节机器人。仿真结果验证了控制器在处理非线性问题方面的有效性,同时最大限度地降低了未知有界干扰的影响。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Robust model predictive control of sampled-data Lipschitz nonlinear systems: Application to flexible joint robots
Controlling flexible joint robots has drawn the attention of many industry professionals during the past two decades. It is a difficult task because various structural features that make the control of rigid robots easier, such as passivity of the motor torque to link velocity, full actuation, and separate control of each joint, are lost when we consider joint flexibility in the control design of these robots. However, we must consider joint flexibility while designing the controller; otherwise, the system may become unstable. In this article, we devise a robust model predictive controller scheme for flexible joint robots modeled as sampled-data Lipschitz nonlinear systems with unknown bounded disturbances. It is assumed that the state of the system is accessible for feedback. Therefore, a state-feedback control law is designed using a robust stability criterion and can be computed by solving an online optimization problem. The control law optimizes the performance index by reducing its worst-case value. The proposed control design scheme is applied to the one-link flexible joint robot. Simulation results validate the effectiveness of the controller in handling nonlinearities while minimizing the effect of unknown bounded disturbances.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

European Journal of Control
工程技术-自动化与控制系统
CiteScore
5.80
自引率
5.90%
发文量
131
审稿时长
1 months
期刊介绍:
The European Control Association (EUCA) has among its objectives to promote the development of the discipline. Apart from the European Control Conferences, the European Journal of Control is the Association''s main channel for the dissemination of important contributions in the field.
The aim of the Journal is to publish high quality papers on the theory and practice of control and systems engineering.
The scope of the Journal will be wide and cover all aspects of the discipline including methodologies, techniques and applications.
Research in control and systems engineering is necessary to develop new concepts and tools which enhance our understanding and improve our ability to design and implement high performance control systems. Submitted papers should stress the practical motivations and relevance of their results.
The design and implementation of a successful control system requires the use of a range of techniques:
Modelling
Robustness Analysis
Identification
Optimization
Control Law Design
Numerical analysis
Fault Detection, and so on.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


