优化宽带激发和再聚焦的 EPR 脉冲
IF 2
3区 化学
Q3 BIOCHEMICAL RESEARCH METHODS
引用次数: 0
摘要
在本文中,我们通过数值方法优化了能使哈恩回波幅度最大化的宽带脉冲形状。脉冲参数为神经网络(NN)、非线性幅度限制傅里叶级数(FS)和离散时间级数(DT)。这些参数与传统双曲正割(HS)脉冲形状的优化选择进行了比较。由于功率放大器的非线性和微波谐振器的传递函数,还包括功率约束和实际的形状失真。我们发现,NN、FS 和 DT 参数化的性能相当,比最佳 HS 脉冲有所改进,并包含大量等效的最优最大值,这意味着在未来的设计中可以灵活地加入更多的约束条件或优化目标。本文章由计算机程序翻译,如有差异,请以英文原文为准。
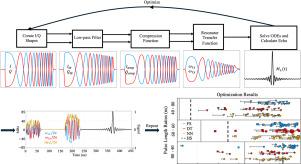
Optimizing EPR pulses for broadband excitation and refocusing
In this paper, we numerically optimize broadband pulse shapes that maximize Hahn echo amplitudes. Pulses are parameterized as neural networks (NN), nonlinear amplitude limited Fourier series (FS), and discrete time series (DT). These are compared to an optimized choice of the conventional hyperbolic secant (HS) pulse shape. A power constraint is included, as are realistic shape distortions due to power amplifier nonlinearity and the transfer function of the microwave resonator. We find that the NN, FS, and DT parameterizations perform equivalently, offer improvements over the best HS pulses, and contain a large number of equivalent optimal maxima, implying the flexibility to include further constraints or optimization goals in future designs.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
3.80
自引率
13.60%
发文量
150
审稿时长
69 days
期刊介绍:
The Journal of Magnetic Resonance presents original technical and scientific papers in all aspects of magnetic resonance, including nuclear magnetic resonance spectroscopy (NMR) of solids and liquids, electron spin/paramagnetic resonance (EPR), in vivo magnetic resonance imaging (MRI) and spectroscopy (MRS), nuclear quadrupole resonance (NQR) and magnetic resonance phenomena at nearly zero fields or in combination with optics. The Journal''s main aims include deepening the physical principles underlying all these spectroscopies, publishing significant theoretical and experimental results leading to spectral and spatial progress in these areas, and opening new MR-based applications in chemistry, biology and medicine. The Journal also seeks descriptions of novel apparatuses, new experimental protocols, and new procedures of data analysis and interpretation - including computational and quantum-mechanical methods - capable of advancing MR spectroscopy and imaging.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


