抗病毒治疗后病毒反弹的理论:SARS-CoV-2 研究案例。
IF 1.9
4区 数学
Q2 BIOLOGY
引用次数: 0
摘要
部分感染 SARS-CoV-2 的患者在接受有效的抗病毒药物(如 Nirmatrelvir/Ritonavir(Paxlovid))治疗后,病情出现反弹。虽然人们已经从生物学和统计学的角度对这一现象进行了研究,但对其背后的动力学机制尚未完全了解。在这项工作中,我们从集合论稳定性分析的角度描述了靶细胞模型的动态行为,以解释治疗后的反弹。在不依赖适应性免疫系统或病毒变异产生的抗药性的情况下,我们为抗病毒治疗提出了避免病毒反弹的数学条件。模拟结果表明了剂量(即给药剂量和时机)在利用高效药物和定制疗法方面的关键作用。本文章由计算机程序翻译,如有差异,请以英文原文为准。
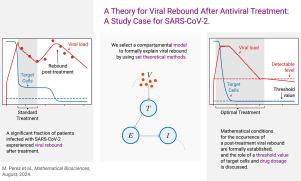
A theory for viral rebound after antiviral treatment: A study case for SARS-CoV-2
A fraction of individuals infected with SARS-CoV-2 experienced rebounds when treated with effective antivirals such as Nirmatrelvir/Ritonavir (Paxlovid). Although this phenomenon has been studied from biological and statistical perspectives, the underlying dynamical mechanism is not yet fully understood. In this work, we characterize the dynamic behavior of a target-cell model to explain post-treatment rebounds from the perspective of set-theoretic stability analysis. Without relying on the effects of the adaptive immune system or the resistance through viral mutations, we develop mathematical conditions for antiviral treatments to avoid viral rebound. Simulation results illustrate the critical role of dosage (i.e., the doses and timing of administration) in taking advantage of highly effective drugs and tailoring therapies.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Mathematical Biosciences
生物-生物学
CiteScore
7.50
自引率
2.30%
发文量
67
审稿时长
18 days
期刊介绍:
Mathematical Biosciences publishes work providing new concepts or new understanding of biological systems using mathematical models, or methodological articles likely to find application to multiple biological systems. Papers are expected to present a major research finding of broad significance for the biological sciences, or mathematical biology. Mathematical Biosciences welcomes original research articles, letters, reviews and perspectives.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


