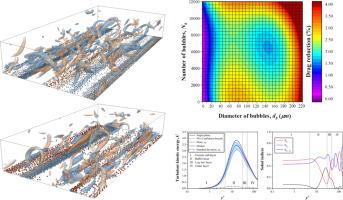
Uncertainty quantification for the drag reduction of microbubble-laden fluid flow in a horizontal channel

Over three decades, much research has proven the bubble drag reduction (BDR) technique. Recently, the improvement of computing performance has enabled the simulation of multi-phase flows. The present work simulated the microbubble-laden turbulent horizontal channel flow by Nek5000 code, which is based on the spectral element method. To resolve the microbubble dynamics, the 2-way coupling Euler–Lagrange approach was combined with Nek5000 code. Furthermore, for high accuracy, high-order Lagrange interpolation was adopted to track the microbubble's location and velocity in this code. All microbubbles were assumed as non-deformable, spherical, and immiscible. For the investigation of the drag reduction effect of microbubble size and the number of microbubbles, the uncertainty quantification (UQ) method was adopted with the non-intrusive polynomial chaos method. The Latin hypercube sampling method was used to obtain precision with lesser number of samples than the Monte Carlo method. The distribution of random variables was assumed to be Gaussian and generalized polynomial chaos expansion (gPC) was applied to build the surrogate model. The mean value (μ) of random variables was 110 µm, 6,345 each, while the standard deviation (σ) was ± 0.33 μ. As a result, the uncertainty propagation of velocity, second-order turbulence statistics, and drag reduction were achieved.