底部地形和表面活性剂作用下的薄液膜稳定性
IF 3.6
2区 工程技术
Q1 MECHANICS
International Journal of Multiphase Flow
Pub Date : 2024-11-02
DOI:10.1016/j.ijmultiphaseflow.2024.105043
引用次数: 0
摘要
我们考虑了在表面活性剂存在的情况下,重力驱动流体沿波浪形倾斜表面向下流动的问题。底部地形的周期性使我们能够利用 Floquet 理论来确定线性化控制偏微分方程的解的形式。结果表明,从稳态开始的扰动是波浪式的,并且确定了一种分散关系,它将初始扰动的波数 κ 与其复频 ω 联系起来。ω的实部提供了确定线性流动稳定性的标准。我们观察到,添加表面活性剂通常会对流动产生稳定作用,但在小波数情况下会产生不稳定作用。这些结果与非线性系统的数值模拟进行了比较和验证。线性分析和非线性分析结果显示出良好的一致性,除了在小波数时,线性分析结果无法复制。本文章由计算机程序翻译,如有差异,请以英文原文为准。
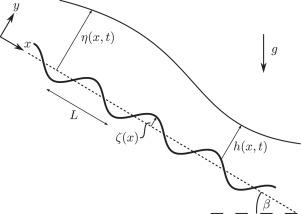
Thin liquid film stability in the presence of bottom topography and surfactant
We consider gravity-driven fluid flow down a wavy inclined surface in the presence of surfactant. The periodicity of the bottom topography allows us to leverage Floquet theory to determine the form of the solution to the linearized governing partial differential equations. The result is that perturbations from steady state are wavelike, and a dispersion relation is identified which relates the wavenumber of an initial perturbation, , to its complex frequency, . The real part of provides a criterion for determining linear flow stability. We observe that the addition of surfactant generally has a stabilizing effect on the flow, but has a destabilizing effect for small wavenumbers. These results are compared and validated against numerical simulations of the nonlinear system. The linear and nonlinear analyses show good agreement, except at small wavenumbers, where the linear results could not be replicated.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
7.30
自引率
10.50%
发文量
244
审稿时长
4 months
期刊介绍:
The International Journal of Multiphase Flow publishes analytical, numerical and experimental articles of lasting interest. The scope of the journal includes all aspects of mass, momentum and energy exchange phenomena among different phases such as occur in disperse flows, gas–liquid and liquid–liquid flows, flows in porous media, boiling, granular flows and others.
The journal publishes full papers, brief communications and conference announcements.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


