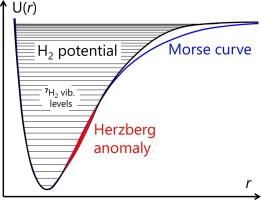
Elucidating the isotope effect in the Morse approximation of the ground state electronic term of hydrogen molecules nH2, n = 1 ÷ 7. Showcasing the Herzberg anomaly and anharmonicity

The Morse function is the simplest anharmonic approximation of the potential of a diatomic molecule, for which the vibrational Schrödinger equation could be solved almost precisely. Despite its crudeness, the Morse function has been widely used in solving various problems in molecular spectroscopy. In recent years, special attention was paid to the existence of two Morse approximations for the electronic terms U(r) of diatomic molecules, M1(r) and M2(r), which differ by the selection of primary fitting parameters and satisfactorily reproduce different parts of U(r). Some fine features of simple terms U(r), whose form does not differ much from the Morse function, could be highlighted by considering difference functions U(r) − M(r). The set of vibrational levels G(υ), predicted by Morse approximation, can be conveniently characterized by the difference functions Δ₁G(υ) and Δ₂G(υ), which are, respectively, the energies of vibrational quanta and the rates of their change. The function Δ₂G(υ) can be considered as a generalization of the anharmonicity constant, determined experimentally by the position of levels υ = 0,1,2. Finally, analysing the anharmonicity, it is useful to compare the results obtained for various isotopologues, for which U(r) is the same, but the density of vibrational levels is different. The maximal range of isotope effects is expected for hydrogen, which has seven known isotopes, including extremely short-lived ones. In this work, the influence of the reduced mass on the results of the approximation of the ground state electronic potential U(r) by the Morse function is studied for seven isotopologues of hydrogen molecule ⁿH₂ (n = 1–7). For each isotopologue, alternative approximations M1(r) and M2(r) are considered. The systematic deviation of M1(r) from U(r) increases with r, reaching 1700–2770 cm⁻¹ (for ⁷H₂–¹H₂) in the region of the asymptote. The systematic deviation of M2(r) from U(r) decreases at larger distances: it is dome-shaped with a maximum of ca. 1500 cm⁻¹ at r ∼ 2 Å, after which it falls to zero. The M2(r) curves for different isotopologues diverge by less than 20 cm⁻¹. The U(r) − M(r) functions are used to analyse the so-called “Herzberg anomaly” in the region where M1(r) and M2(r) intersect U(r). For example, at around r = 1.08 Å the U(r) − M2(r) function shows anomalous negative values ranging from −125 cm⁻¹ (for ¹H₂) to −142 cm⁻¹ (for ⁷H₂).