考奇辐射规中麦克斯韦理论的量子化：霍奇分解与哈达玛态

IF 1 2区数学 Q1 MATHEMATICS

Journal of the London Mathematical Society-Second Series Pub Date : 2024-11-05 DOI:10.1112/jlms.70020

Simone Murro, Gabriel Schmid

{"title":"考奇辐射规中麦克斯韦理论的量子化：霍奇分解与哈达玛态","authors":"Simone Murro, Gabriel Schmid","doi":"10.1112/jlms.70020","DOIUrl":null,"url":null,"abstract":"The aim of this paper is to prove the existence of Hadamard states for the Maxwell equations on any globally hyperbolic spacetime. This will be achieved by introducing a new gauge fixing condition, the Cauchy radiation gauge, that will allow to suppress all the unphysical degrees of freedom. The key ingredient for achieving this gauge is a new Hodge decomposition for differential <math>\n <semantics>\n <mi>k</mi>\n <annotation>$k$</annotation>\n </semantics></math>-forms in Sobolev spaces on complete (possibly noncompact) Riemannian manifolds.","PeriodicalId":49989,"journal":{"name":"Journal of the London Mathematical Society-Second Series","volume":null,"pages":null},"PeriodicalIF":1.0000,"publicationDate":"2024-11-05","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.70020","citationCount":"0","resultStr":"{\"title\":\"The quantization of Maxwell theory in the Cauchy radiation gauge: Hodge decomposition and Hadamard states\",\"authors\":\"Simone Murro, Gabriel Schmid\",\"doi\":\"10.1112/jlms.70020\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"The aim of this paper is to prove the existence of Hadamard states for the Maxwell equations on any globally hyperbolic spacetime. This will be achieved by introducing a new gauge fixing condition, the Cauchy radiation gauge, that will allow to suppress all the unphysical degrees of freedom. The key ingredient for achieving this gauge is a new Hodge decomposition for differential <math>\\n <semantics>\\n <mi>k</mi>\\n <annotation>$k$</annotation>\\n </semantics></math>-forms in Sobolev spaces on complete (possibly noncompact) Riemannian manifolds.\",\"PeriodicalId\":49989,\"journal\":{\"name\":\"Journal of the London Mathematical Society-Second Series\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":1.0000,\"publicationDate\":\"2024-11-05\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.70020\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of the London Mathematical Society-Second Series\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://onlinelibrary.wiley.com/doi/10.1112/jlms.70020\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of the London Mathematical Society-Second Series","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/jlms.70020","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

本文旨在证明麦克斯韦方程在任何全局双曲时空中的哈达玛德状态的存在性。这将通过引入一种新的量规固定条件--考奇辐射量规来实现，该量规可以抑制所有非物理自由度。实现这一量规的关键要素是完整（可能非紧凑）黎曼流形上索博列夫空间中微分 k $k$ 形式的新霍奇分解。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

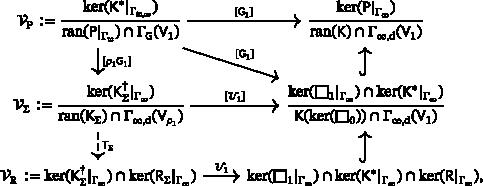
The quantization of Maxwell theory in the Cauchy radiation gauge: Hodge decomposition and Hadamard states

The aim of this paper is to prove the existence of Hadamard states for the Maxwell equations on any globally hyperbolic spacetime. This will be achieved by introducing a new gauge fixing condition, the Cauchy radiation gauge, that will allow to suppress all the unphysical degrees of freedom. The key ingredient for achieving this gauge is a new Hodge decomposition for differential $k$ -forms in Sobolev spaces on complete (possibly noncompact) Riemannian manifolds.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of the London Mathematical Society-Second Series 数学-数学

CiteScore

1.90

自引率

0.00%

发文量

186

审稿时长

6-12 weeks

期刊介绍： The Journal of the London Mathematical Society has been publishing leading research in a broad range of mathematical subject areas since 1926. The Journal welcomes papers on subjects of general interest that represent a significant advance in mathematical knowledge, as well as submissions that are deemed to stimulate new interest and research activity.