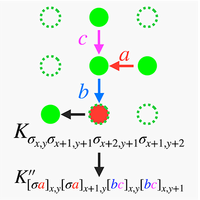
Initial tensor construction and dependence of the tensor renormalization group on initial tensors

We propose a method to construct a tensor network representation of partition functions without singular value decompositions nor series expansions. The approach is demonstrated for one- and two-dimensional Ising models and we study the dependence of the tensor renormalization group (TRG) on the form of the initial tensors and their symmetries. We further introduce variants of several tensor renormalization algorithms. Our benchmarks reveal a significant dependence of various TRG algorithms on the choice of initial tensors and their symmetries. However, we show that the boundary TRG technique can eliminate the initial tensor dependence for all TRG methods. The numerical results of TRG calculations can thus be made significantly more robust with only a few changes in the code. Furthermore, we study a three-dimensional ℤ2 gauge theory without gauge fixing and confirm the applicability of the initial tensor construction. Our method can straightforwardly be applied to systems with longer range and multisite interactions, such as the next-nearest neighbor Ising model.